Problème du cavalier - Définition
Le problème ou polygraphie, ou encore algorithme du cavalier est un problème mathématico-logique qui suit les déplacements du cavalier (dit en L, deux cases en avant et une sur le côté).
Un cavalier doit visiter toutes les cases de l'échiquier une seule fois, quelle que soit sa case de départ.
Le cavalier d'Euler est connu depuis fort longtemps. Vers 840, al-Adli ar-Rumi en donne déjà une solution. On en trouve la première occurrence dans un traité d'ornement poétique indien, le Kavyalankara du poète Rudrata. Le mathématicien Leonhard Euler est cependant le premier à l'avoir étudié scientifiquement en 1759. La " Solution d'une question curieuse qui ne paraît soumise à aucune analyse " n'est cependant publié qu'en 1766. Côme Alexandre Collini (1727 – 1806), secrétaire de Voltaire en publia une dans le Journal Encyclopédique en 1773.
Parmi les milliards de solutions, seules 122 000 000 se terminent à un pas de la case de départ.
Le problème du cavalier est un cas particulier des graphes hamiltoniens dans la théorie des graphes.
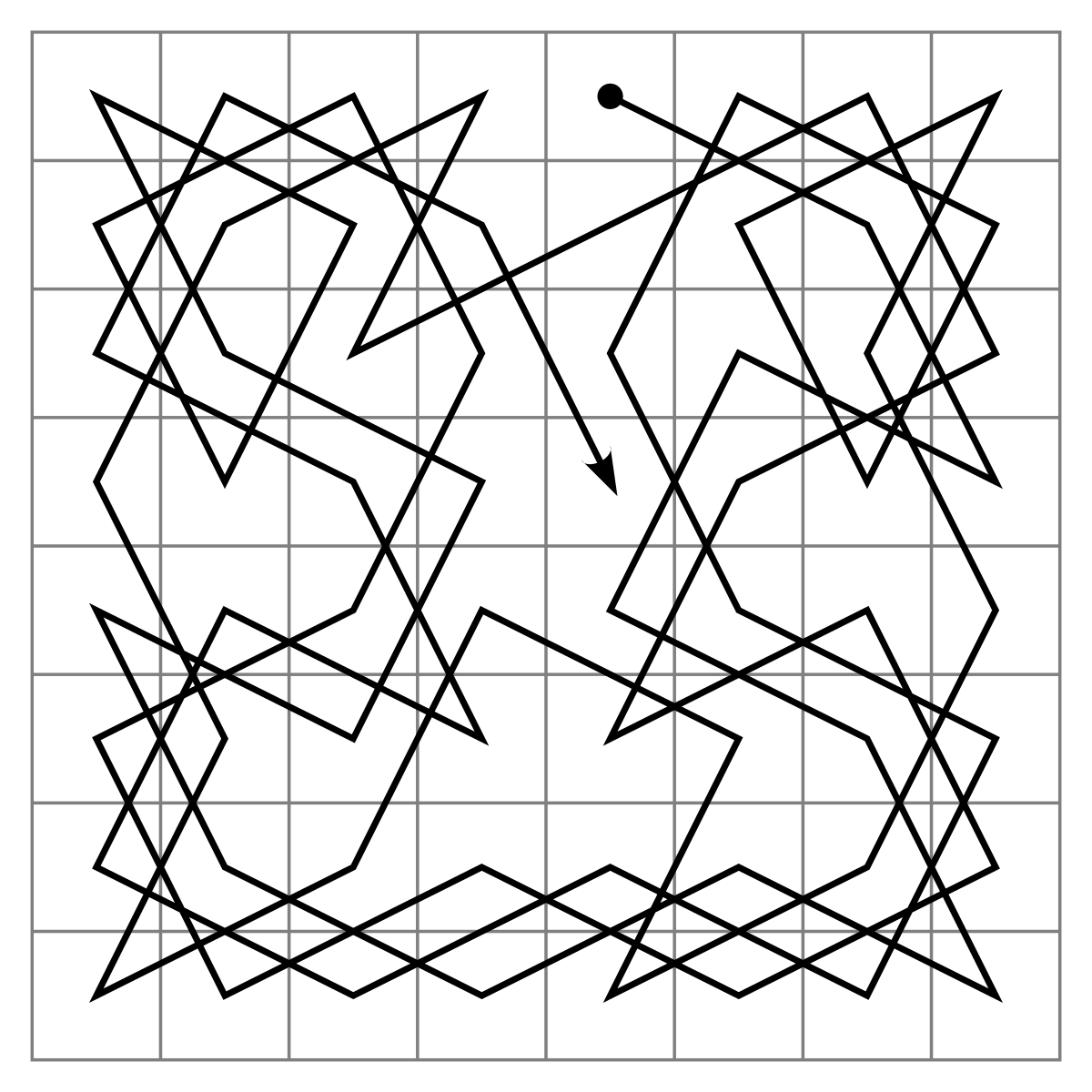
Voici une solution qui permet de parcourir toutes les cases et de revenir à la case de départ, dite fermée.
B1 A3 C2 A1 B3 C1 A2 B4 D5 E7 F5 H4 F3 H2 F1 G3 H1 F2 H3 G1 E2 D4 B5 D6 E8 G7 E6 D8 C6 A7 C8 B6 A8 C7 A6 B8 D7 E5 G4 E3 D1 B2 D3 E1 G2 F4 H5 F6 G8 H6 F7 H8 G6 F8 H7 G5 E4 D2 C4 A5 B7 C5 A4 C3 et retour en B1
La représentation graphique de ce parcours décrit une très jolie arabesque.
Au fil des siècles, les mathématiciens étudient ce thème en variant :
- les dimensions de l'échiquier,
- le nombre de joueurs,
- la façon dont un cavalier se déplace.
Au XXe siècle, le groupe d'écrivains Oulipo utilise ce problème. L'exemple le plus remarquable est le tour 10x10 qui détermine l'ordre des chapitres dans le livre de Georges Perec : La Vie mode d'emploi. Il a également utilisé par le même auteur un 9x9 dans Deux cent quarante-trois cartes postales en couleurs véritables.
Variante
Les tours de cavaliers peuvent aussi être sur des damiers de différente taille ; mais pas seulement que sur des damiers. les formes ou le cavalier va pouvoir évoluer peut être sur d'autres formes (rectangle, cube, , pavé , spirale infinie...)
Un cavalier ne pourra mouvoir dans un pavé de moins de 6x6 et il pourra revenir à son point de départ si et seulement si la forme ou il évolue contient un nombre paire de cases.