Orbite géostationnaire - Définition
L'orbite géostationnaire, abrégée GEO (geostationary orbit), parfois appelée orbite de Clarke, est une orbite située à 35 786 km d'altitude au-dessus de l'équateur de la Terre, dans le plan équatorial et d'une excentricité orbitale nulle. C'est un cas particulier de l'orbite géosynchrone.
Particularité
Sa caractéristique est qu'un corps se trouvant sur cette orbite possède une période de révolution très exactement égale à la période de rotation de la Terre sur elle-même, soit 23h 56m 4s (c'est la caractéristique de l'orbite géosynchrone), et paraît immobile par rapport à tout point à la surface de la Terre.
Cette caractéristique est particulièrement importante pour les satellites de télécommunications ou bien de diffusion de télévision. La position du satellite semblant immobile, un équipement de réception muni d'une antenne fixe pointant dans la direction du satellite géostationnaire suffira pour capter ses émissions. Pour la couverture de l'Europe, c'est principalement Eutelsat qui assure cette mission avec de nombreux satellites en orbite.
Cette orbite est également utilisée pour l'observation de la Terre depuis une position fixe dans l'espace. C'est le cas pour les satellites météorologiques géostationnaires, dont les Meteosat pour l'Europe.
Il est à noter que les satellites géostationnaires sont nécessairement situés à la verticale ou au zénith d'un point de l'équateur ou, en d'autres termes, situés dans le plan équatorial de la Terre. On entend parfois parler abusivement de " satellite géostationnaire au-dessus de l'Europe " : il faut entendre par là satellite en orbite géostationnaire visible depuis l'Europe.
La plupart des corps célestes possèdent une orbite présentant une telle caractéristique.
Calcul de l'altitude de l'orbite géostationnaire
Seconde loi de Newton :
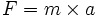
Mouvement circulaire uniforme :
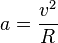
Loi de la gravitation universelle :
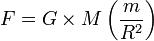
avec :
-

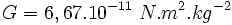
-
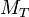
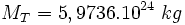
-
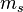
-
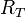
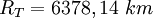
-
-
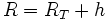
-
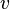
d'où
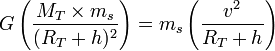
La vitesse, pour une trajectoire circulaire est :
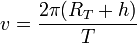
où

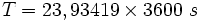
Après calcul on obtient :
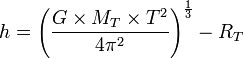
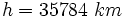
Calcul de la vitesse du satellite
À partir de la seconde loi de Newton et de la loi de la gravitation universelle on peut écrire :
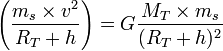
d'où
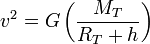
Pour
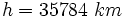
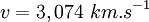
Autre méthode de calcul :
V = (2πR)/ T ou R est la distance du centre de la Terre au satellite (en mètres), soit:
R = rayon de la Terre Rt + altitude du satellite h
R = Rt + h
et T est la période des satellites geostationnaires soit 86 164 s
V= (2π x 4,2162x10^7) / 86164 = 3074m/s