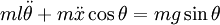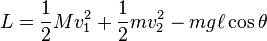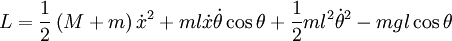Pendule inversé - Définition

En physique, un pendule inversé est un pendule simple. Il présente une position d'équilibre instable s'il est maintenu vertical à 180°, mais cette position est maintenue par un système de contrôle ou par excitation de Kapitza. C'est un problème de physique non-linéaire.

Équation du mouvement

La situation est exactement la même que celle décrite pour le pendule simple, en considérant une tige rigide mais de masse négligeable. On définit donc :

• θ l'angle formé entre la tige et la verticale ;
• m la masse du pendule ;
• l la longueur de la tige ;
• g l'accélération de la pesanteur ;

On note les dérivées temporelles par un point :

et .

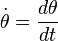
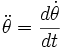
On peut alors établir la période des oscillations :

.

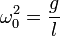
L'énergie cinétique est :

.

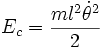
L'énergie potentielle de gravité :

E_p = mgl(1 − cosθ).

Si le pendule est laissé libre, on peut écrire la conservation de l'énergie mécanique, E = E_c + E_p. Alors, on obtient :

.

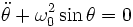
La différence avec le pendule simple est que l'on s'intéresse à la situation θ ≈ π [2π] ; cela correspond à un maximum de l'énergie potentielle, c'est-à-dire à un équilibre instable.

Pendule inversé sur un chariot

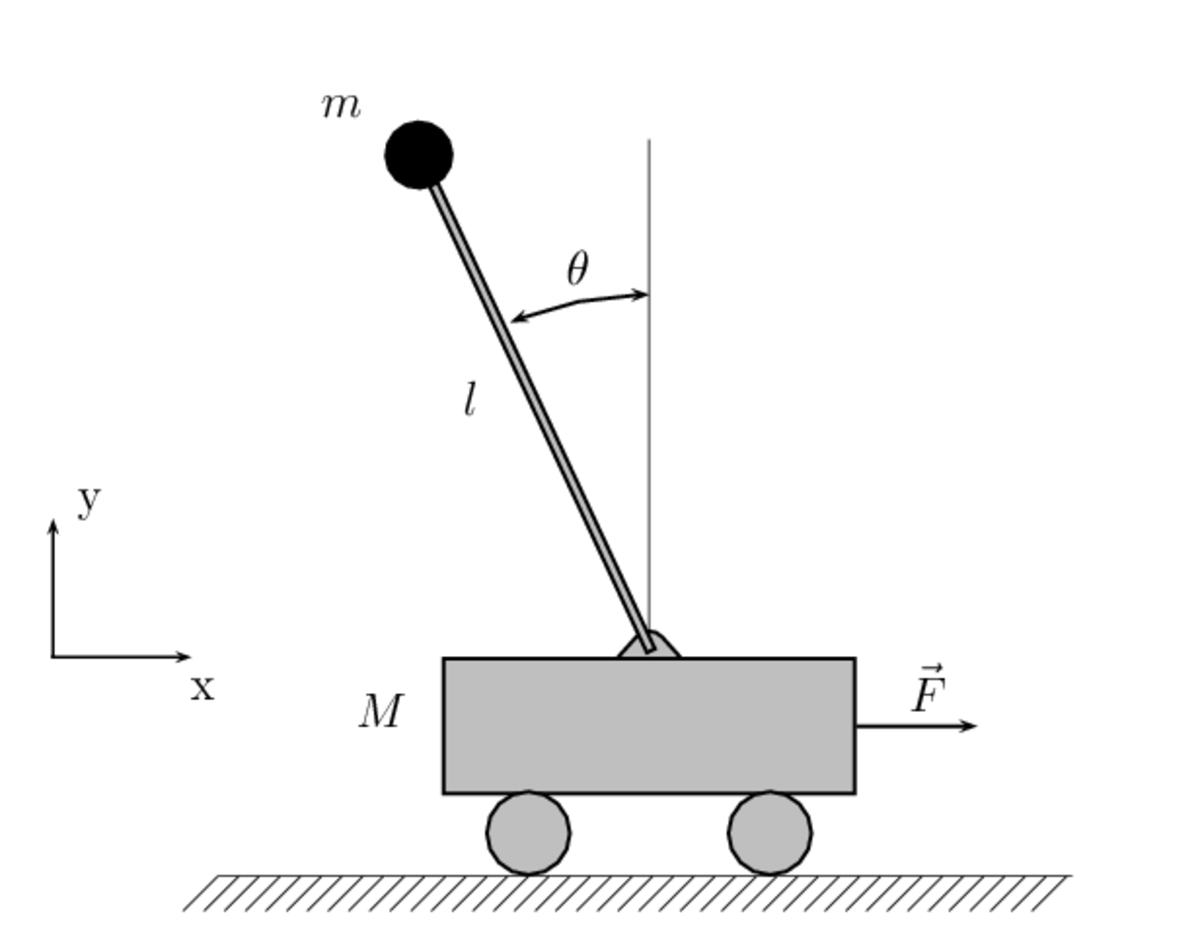
Un pendule inversé sur un chariot.

On peut établir les équations du mouvement à partir de la mécanique lagrangienne : en notant x(t) la position du chariot, θ(t) l'angle formé entre la tige et la verticale, le système étant soumis à la gravité et à une force F, extérieure et selon l'axe x, le lagrangien est :

L = T − V

avec T l'énergie cinétique et V l'énergie potentielle. On a ainsi :

avec v₁ la vitesse du chariot et v₂ celle de la masse m. On peut exprimer v₁ et v₂ à partir de x et θ :

et

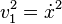
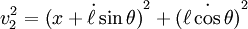
ce qui s'écrit encore :

.

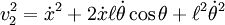
Le lagrangien est donné par :

et les équations du mouvement sont donc :

 ;

.

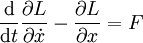
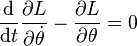
En simplifiant ces équations, on obtient les équations, non-linéaires, du mouvement du pendule :

 ;

.