Algèbre classique - Définition

Introduction

L'algèbre élémentaire ou algèbre classique est la branche des mathématiques dont l'objet est l'étude des opérations algébriques (addition, multiplication, soustraction, division et extraction de racine) sur les nombres réels ou complexes, et dont l'objectif principal est la résolution d'équations polynomiales.

Le qualificatif d'élémentaire (ou classique) est destiné à la différencier de l'algèbre générale (ou moderne), qui étudie les structures algébriques (groupes, corps, etc.) généralisant les notions de nombre et d'opération. Elle se différencie également de l'arithmétique élémentaire par l'usage de lettres pour représenter les nombres inconnus.

En ce sens, l'adjectif algébrique peut, suivant les cas, être un synonyme de polynomial (comme dans courbe algébrique) ou l'antonyme d'arithmétique.

Expressions algébriques

Une expression algébrique est constituée de nombres, de lettres et de signes opératoires :

• le signe + est utilisé pour marquer l'addition.
• le signe − est utilisé pour marquer la soustraction.
• les signes ou sont utilisés pour marquer la multiplication. Quand la multiplication concerne deux lettres, il est possible d'écrire ab au lieu de .
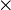
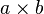
• le signe est utilisé pour marquer la division, pouvant également s'écrire .

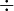
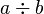
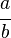
Par exemple :

• Le produit d'un nombre x augmenté de 3 par lui-même s'écrit (x + 3)x.
• La différence des carrés de deux nombres a et b s'écrit a² − b²

Évaluer une expression algébrique consiste à attribuer une valeur à chacune des variables, puis à effectuer le calcul arithmétique obtenu.

Par exemple évaluer l'expression x² + x − 1 pour x = 2 consiste à effectuer le calcul 2² + 2 − 1.

Propriétés de la multiplication

• • est écrit a × b ou a • b;
  • est commutative: a × b = b × a;
  • est associative: (a × b) × c = a × (b × c);
  • est abbrevié par la juxtaposition: a × b ≡ ab;
  • a un élément neutre 1 qui conserve le nombre: a × 1 = a;
  • pour les nombres différents de zero, a une application réciproque appelée division: (ab)/b = a, équivaut à multiplier par son inverse, a/b = a(1/b);
  • est distributive par rapport à l'addition: (a + b)c = ac + bc;

Propriétés de l'addition

• • est écrit a + b;
  • est commutative: a + b = b + a;
  • est associative: (a + b) + c = a + (b + c);
  • a une application réciproque appelée soustraction: (a + b) − b = a, équivaut à additionner un nombre négatif, a − b = a + (−b);
  • a un élément neutre 0 qui conserve le nombre: a + 0 = a.

Bibliographie

Ouvrages

• Amy Dahan-Dalmedico et Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986  
• Ahmed Djebbar, L'algèbre arabe, genèse d'un art, Vuibert/Adapt, 2005, 214 p. .
  Tour d'horizon de l'algèbre arabe, des origines au XV^e siècle.
   

Articles d'encyclopédies

• (en) Yu. I. Merzlyakov et A.I. Shirshov, « Algebra », dans Encyclopaedia of Mathematics, Springer, 2001  
• « Algèbre », dans Encyclopédie Larousse, {{{année}}}  
• « Algèbre », dans Encyclopédie Microsoft® Encarta® en ligne, 2009  

Factorisation et développement

Factoriser une expression algébrique, E, consiste à en transformer l'écriture sous la forme d'un produit de deux ou plusieurs expressions (A, B, ...) :

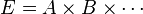
Chacune des expressions A, B, ... est appelée un facteur.

Développer une expression algébrique, E, consiste à en transformer l'écriture sous la forme d'une somme (ou différence) de deux ou plusieurs expressions. (A, B, ...) :

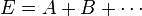
Chacune des expressions A, B, ... est appelée un terme.