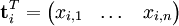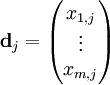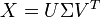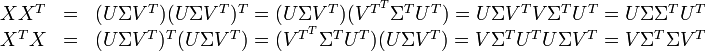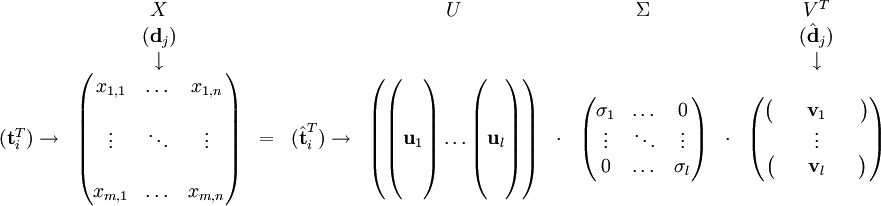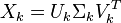Analyse sémantique latente - Définition

Implémentations

La décomposition en valeurs singulières est généralement calculée par des méthodes optimisées pour les matrices larges — par exemple l'algorithme de Lanczos — par des programmes itératifs, ou encore par des réseaux de neurones, cette dernière approche ne nécessitant pas que l'intégralité de la matrice soit gardée en mémoire.

Description

Construction de la matrice des occurrences

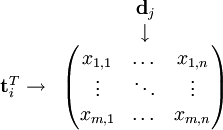
Soit X la matrice où l'élément (i, j) décrit les occurrences du terme i dans le document j — par exemple la fréquence. Alors X aura cette allure :

Une ligne de cette matrice est ainsi un vecteur qui correspond à un terme, et dont les composantes donnent sa présence (ou plutôt, son importance) dans chaque document :

De même, une colonne de cette matrice est un vecteur qui correspond à un document, et dont les composantes sont l'importance dans son propre contenu de chaque terme.

Corrélations

Le produit scalaire :

entre deux vecteurs « termes » donne la corrélation entre deux termes sur l'ensemble du corpus. Le produit matriciel XX^T contient tous les produits scalaires de cette forme : l'élément (i, p) — qui est le même que l'élément (p, i) car la matrice est symétrique — est ainsi le produit scalaire :

( ).

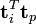
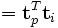
De même, le produit X^TX contient tous les produits scalaires entre les vecteurs « documents », qui donnent leurs corrélations sur l'ensemble du lexique :

.

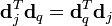
Décomposition en valeurs singulières

On effectue alors une décomposition en valeurs singulières sur X, qui donne deux matrices orthonormales U et V et une matrice diagonale Σ. On a alors :

Les produits de matrice qui donnent les corrélations entre les termes d'une part et entre les documents d'autre part s'écrivent alors :

Puisque les matrices :

ΣΣ^T et Σ^TΣ

sont diagonales, U est faite des vecteurs propres de XX^T, et V est faite des vecteurs propres de X^TX. Les deux produits ont alors les mêmes valeurs propres non-nulles — qui correspondent aux coefficients diagonaux non-nuls de ΣΣ^T. La décomposition s'écrit alors :

Les valeurs sont les valeurs singulières de X. D'autre part, les vecteurs et sont respectivement singuliers à gauches et à droite.

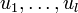
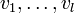
On remarque également que la seule partie de U qui contribue à est la i ^ième ligne. On note désormais ce vecteur . De même la seule partie de V^T qui contribue à est la j ^ième colonne, que l'on note .

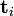
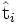
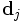
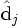
Espace des concepts

Lorsqu'on sélectionne les k plus grandes valeurs singulières, ainsi que les vecteurs singuliers correspondants dans U et V, on obtient une approximation de rang k de la matrice des occurrences.

Le point important, c'est qu'en faisant cette approximation, les vecteurs « termes » et « documents » sont traduits dans l'espace des « concepts ».

Le vecteur possède alors k composantes, qui chacune donne l'importance du terme i dans chacun des k différents « concepts ». De même, le vecteur donne l'intensité des relations entre le document j et chaque concept. On écrit cette approximation sous la forme suivante :

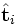
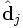
On peut alors effectuer les opérations suivantes :

• voir dans quelle mesure les documents j et q sont liés, dans l'espace des concepts, en comparant les vecteurs et . On peut faire cela en évaluant la similarité cosinus, qui peut se calculer ainsi :

 ;

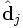
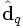
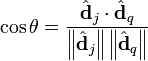
• comparer les termes i et p en comparant les vecteurs et par la même méthode ;
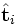
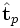
• une requête étant donnée, on peut la traiter comme un « mini-document » et la comparer dans l'espace des concepts à un corpus pour construire une liste des documents les plus pertinents. Pour faire cela, il faut déjà traduire la requête dans l'espace des concepts, en la transformant de la même manière que les documents. Si la requête est q, il faut calculer :

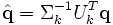
avant de comparer ce vecteur au corpus.