Anneau euclidien - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Propriétés des anneaux euclidiens
Dans la suite de l'article, A est un anneau commutatif unitaire et intègre.
-
- Un anneau euclidien est principal.
Plus précisément, si v est un préstathme sur l'anneau euclidien A, si J est un idéal non nul de A, J admet pour générateur tout élément de J - {0} dont la valeur par le préstathme v est minimale.
Soit b un élément de J - {0} dont la valeur par v est minimale. Prouvons que b est un générateur de J. Soit a un élément de J. Il s'agit de prouver que a est multiple de b. Puisque v est un préstathme euclidien, il existe des éléments q et r de A tels que
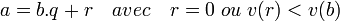
Puisque a et b sont tous deux des éléments de J, r en est un aussi; si r n'était pas nul, on aurait donc
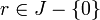
En revanche, un anneau principal n'est pas toujours euclidien, l'article Anneau principal présente un contre-exemple.
Un anneau euclidien possède toutes les propriétés de divisibilité des anneaux principaux : il est factoriel, le lemme d'Euclide, le théorème fondamental de l'arithmétique et l'identité de Bézout sont vérifiés et les opérations sur le plus grand commun diviseur et le plus petit commun multiple s'appliquent.
Si on dispose d'un algorithme effectif de division euclidienne, comme par exemple pour Z ou pour les polynômes à coefficients dans un corps, on peut définir des algorithmes effectifs fournissant explicitement des objets dont l'existence reste théorique dans un cadre plus général. Ainsi l'algorithme d'Euclide se généralise et permet de trouver un générateur de la somme de deux idéaux (autrement dit, permet de trouver un plus grand commun diviseur de deux éléments). De même, le Théorème des facteurs invariants permet de trouver une base d'un A-module de type fini.
Remarque : Pour prouver qu'un anneau euclidien est principal, nous avons seulement utilisé l'existence d'un préstathme et non celle d'un stathme, ce qui explique que certains auteurs ne s'intéressent qu'aux préstathmes (qu'ils appellent stathmes). Toutefois, la preuve du fait qu'un anneau principal est factoriel repose (quant à l'existence de la décomposition en produits d'éléments irréductibles) sur l'axiome du choix. Dans le cas d'un anneau euclidien, l'existence d'un stathme (et non seulement d'un préstathme) permet de prouver sans recours à l'axiome du choix que l'anneau est factoriel.
-
- Tout anneau euclidien est factoriel :
Soit A un anneau euclidien; choisissons un stathme v sur A. Supposons que, par absurde, il existe un élément non nul non inversible de A qui ne soit pas décomposable en produit d'éléments irréductibles. Considérons-en un, soit x, tel que v(x) soit le plus petit possible. Puisque x n'est pas décomposable, il n'est pas irréductible, donc il est produit de deux de ses diviseurs stricts, tous deux non inversibles. (Nous convenons d'entendre par diviseur strict d'un élément x un diviseur de x qui n'en est pas multiple, autrement dit un élément d tel que x soit de la forme dx' avec x' non inversible.) Puisque x n'est pas décomposable, un au moins de ces deux diviseurs, soit y, est indécomposable. Mais y étant diviseur strict de x, nous avons, d'après une propriété des stathmes (voir la section correspondante), v(y) < v(x), ce qui contredit la minimalité de v(x). Cette contradiction prouve l'existence de la décomposition en produit d'éléments irréductibles. L'unicité se démontre sans recours à l'axiome du choix, même dans le cas général des anneaux principaux.
Propriétés des stathmes
-
- Soient a et b deux éléments non nuls de A et v un stathme; si v(a.b) = v(a), alors b est un élément du groupe des unités.
Il revient au même de prouver que si x et y sont des éléments non nuls de A, si x est diviseur strict de y (c'est-à-dire si x divise y sans en être multiple, autrement dit si y est de la forme xz avec z non inversible), alors v(x) < v(y).
Il existe q et r dans A tels que
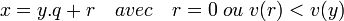
Puisque x est diviseur strict de y, il n'en est pas multiple, donc r n'est pas nul, donc v(r ) < v(y). Mais r est clairement multiple de x, donc, puisque nous supposons v croissant,
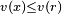
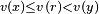
Il est toujours possible de normaliser un stathme v par translation, c'est-à-dire de choisir un stathme w tel que l'image par le stathme d'une unité soit égal à un. Plus précisément, il suffit de définir w par w(x) = v(x) - v(1) + 1 pour tout élément non nul x de A. Dans ce cas :
-
- Un élément non nul u de A est élément du groupe des unités de A si, et seulement si, w(u) = 1. De plus, 1 est la valeur minimale que prend w dans A - {0}.
Si on étend le stathme normalisé w à l'anneau A tout entier en posant w(0) = 0, 0 est le seul élément x de A tel que w(x) = 0, ce qui permet de donner au principe de division euclidienne cette forme un peu plus élégante :
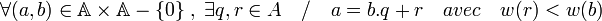
Cette convention n'est pas suivie dans tous les cas. Le stathme dispose de propriétés qui dépassent souvent celles de la division euclidienne. Dans le premier exemple sur Z, le stathme dispose de propriétés métriques, dans le deuxième exemple la fonction degré vérifie une propriété utile : le degré du produit de deux polynômes est égal à la somme des degrés des polynômes. Pour ne pas perdre cette propriété, les unités de l'anneau ont un stathme (degré) choisi égal à zéro et le polynôme nul a pour image (degré) moins l'infini.

















































