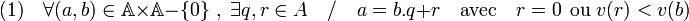Anneau euclidien - Définition
La liste des auteurs de cet article est disponible ici.
Définitions
Il existe certains points communs entre les exemples : l'anneau est toujours commutatif unitaire, intègre et, dans chaque cas, une fonction à valeurs dans N (valeur absolue, degré ou norme) est utilisée pour définir la division euclidienne. Ces fonctions sont des cas particuliers de stathme euclidien. De façon générale, si A désigne un anneau commutatif unitaire et intègre, on pose la définition suivante.
-
- Un stathme euclidien sur A est une application v de A - {0} dans l'ensemble N des entiers positifs vérifiant les deux propriétés :
La condition (2) revient à dire que si A-{0} est muni de la relation de préordre «divise» et N de la relation d'ordre usuelle, l'application v est croissante.
-
- Le terme de préstathme euclidien désigne une application de A - {0} dans N possédant la propriété (1).
-
- Un anneau commutatif unitaire et intègre est dit euclidien si et seulement s'il existe un stathme euclidien sur cet anneau. On parle alors de division euclidienne dans cet anneau par rapport au stathme.
Remarques : 1 ° Certains auteurs utilisent le terme de stathme euclidien pour désigner ce qui est appelé ici un préstathme. La différence n'est pas grande, car s'il existe un préstathme sur A, il existe aussi un stathme.
-
- Soit A un anneau commutatif unitaire intègre muni d'un préstathme v, il existe un stathme w :
Par hypothèse, il existe un préstathme v sur A. Nous allons définir un stathme w. Pour tout élément non nul x de A, désignons par w(x) la plus petite des valeurs v(y), y parcourant les multiples non nuls de x. Puisque x est lui-même un tel y, nous avons :
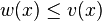
-
-
- Soient a et b deux éléments non nuls de A tels que b divise a, alors w(a) est supérieur ou égal à w(b) :
-
Soient Ea l'ensemble des valeurs v(a') où a' parcourt les multiples non nuls de a et Eb l'ensemble des valeurs v(b') où b' parcourt les multiples non nuls de b. La valeur w(a) est, par définition, le plus petit élément de w(Ea) et w(b) le plus petit élément de w(Eb). Puisque a est multiple de b, l'ensemble Ea est contenu dans l'ensemble Eb, donc inf(Ea), c'est-à-dire w(a), est supérieur ou égal à inf(Eb), c'est-à-dire à w(b).
-
-
- La fonction w est un stathme, c'est-à-dire qu'elle vérifie aussi la condition :
-
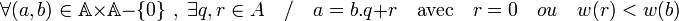
Par définition de w, il existe un élément non nul c0 de A tel que w(b) = v(bc0).
Puisque v est un préstathme, la division euclidienne de a par bc0 relativement à v fournit un couple (q 0, r0 ) d'éléments de A tels que :
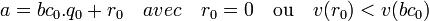
Si r0 est nul, notre thèse est évidemment vraie (avec q = c0q0 et r= 0). Supposons donc r0 non nul. Alors v(r0) est strictement inférieur à v(bc0). Nous avons vu que la fonction w est inférieure ou égale à v, donc w(r0) est inférieur ou égal à v(r0), donc
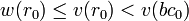
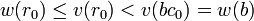
Nous avons obtenu ainsi une "division de a par b" euclidienne par rapport à w, avec pour quotient c0.q 0 et pour reste r0, ce qui achève de prouver notre thèse.
2 ° comme le montrent des exemples donnés dans les cas particuliers introductifs, les éléments q et r de la relation (1) ne sont pas forcément uniques.
Exemples
Entiers relatifs
Les entiers relatifs forment le prototype de l'anneau euclidien. Cet ensemble vérifie la propriété suivante :
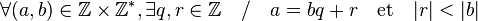
On reconnait là la forme de la division euclidienne dans l'ensemble des entiers naturels N pour laquelle |n| = n. On peut remarquer toutefois que, d'une part N n'est pas un anneau, d'autre part il n'est pas précisé ici l'unicité de q et r. Ceci s'explique par le fait que, pour pouvoir prolonger à Z (ensemble des entiers relatifs) la définition de la division dans N, il faut, ou bien fixer une condition supplémentaire sur b (b > 0) restreignant ainsi le champ de validité de la division euclidienne, ou bien accepter de prendre b négatif et prendre pour définition a = bq + r avec |r| < |b|. Mais alors on peut trouver deux décompositions possibles :
- 19 = (- 5) × (- 3) + 4 avec |4| < |-5| mais aussi 19 =(- 5) × (- 4) + (-1) avec |-1| < |-5|
Cette division permet de bâtir une arithmétique vérifiant les propriétés suivantes :
En conséquence, il est possible de définir : la famille des nombres premiers, le ppcm ainsi que le pgcd. L'anneau quotient Z/nZ est bien défini, il est la structure à la base de l'arithmétique modulaire.
La première application connue est probablement la démonstration de l'irrationalité de la racine carrée de deux. Le petit théorème de Fermat se démontre rapidement une fois établi le fait que si n est premier Z/nZ dispose d'une structure de corps. Fermat utilise largement cette arithmétique, par exemple pour démontrer l'absence de solution pour son grand théorème si n est égal à quatre. Euler donne une large quantité d'exemples d'utilisation de l'arithmétique dans Z, comme l'étude de l'équation de Pell-Fermat.
Ces résultats sont les propriétés qui ont motivé la création de la notion abstraite d'anneau euclidien. En effet, toutes ces propriétés ne sont les conséquences que d'une seule, la division euclidienne.
Polynômes à coefficients dans un corps commutatif

Si un corps K est commutatif, alors l'anneau des polynômes K[X] est euclidien. La division prend la forme suivante :
![\forall A(X), B(X)\in\mathbb{K}[X] \quad \exists ! Q(X), R(X)\in\mathbb{K}[X]](https://static.techno-science.net/illustration/Definitions/autres/5/52fb2a46abd48873e947624e1a7d9b14_2c6deec001f8f6b3ae7161916757e19a.png)
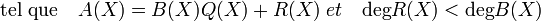
Si la forme est globalement analogue à celle des entiers, on remarque néanmoins qu'une relation d'ordre sur l'ensemble K[X] n'est pas nécessaire. Il suffit d'une application, analogue à celle qui, à un polynôme associe son degré, et dont l'ensemble d'arrivée est ordonné, une telle application est appelée stathme euclidien.
L'arithmétique se fonde sur les mêmes conséquences, l'anneau est principal, l'identité de Bézout est vérifiée, le lemme d'Euclide et le théorème fondamental de l'arithmétique s'appliquent. Les équivalents des nombres premiers sont les polynômes irréductibles, c’est-à-dire ceux qui n'ont pour diviseurs qu'eux-mêmes ou l'unité à une constante multiplicative près. La décomposition en polynômes irréductibles est la factorisation la plus complète possible.
L'équivalent de l'arithmétique modulaire se focalise sur les anneaux quotientés par des idéaux premiers (c’est-à-dire des idéaux engendrés par des polynômes irréductibles). Comme précédemment ces idéaux possèdent une structure de corps. Les quotients sont appelés corps de rupture car se sont les plus petits corps contenant une racine du polynôme. Cette approche, permettant de définir une extension finie du corps K définit l'outil de base de la théorie de Galois.
Un exemple d'application est le suivant : les polynômes cyclotomiques correspondent à la décomposition en facteurs irréductibles du polynôme des racines de l'unité Xn - 1. L'analyse de ces polynômes permet de déterminer tous les polygones constructibles à la règle et au compas.
Entiers de Gauss
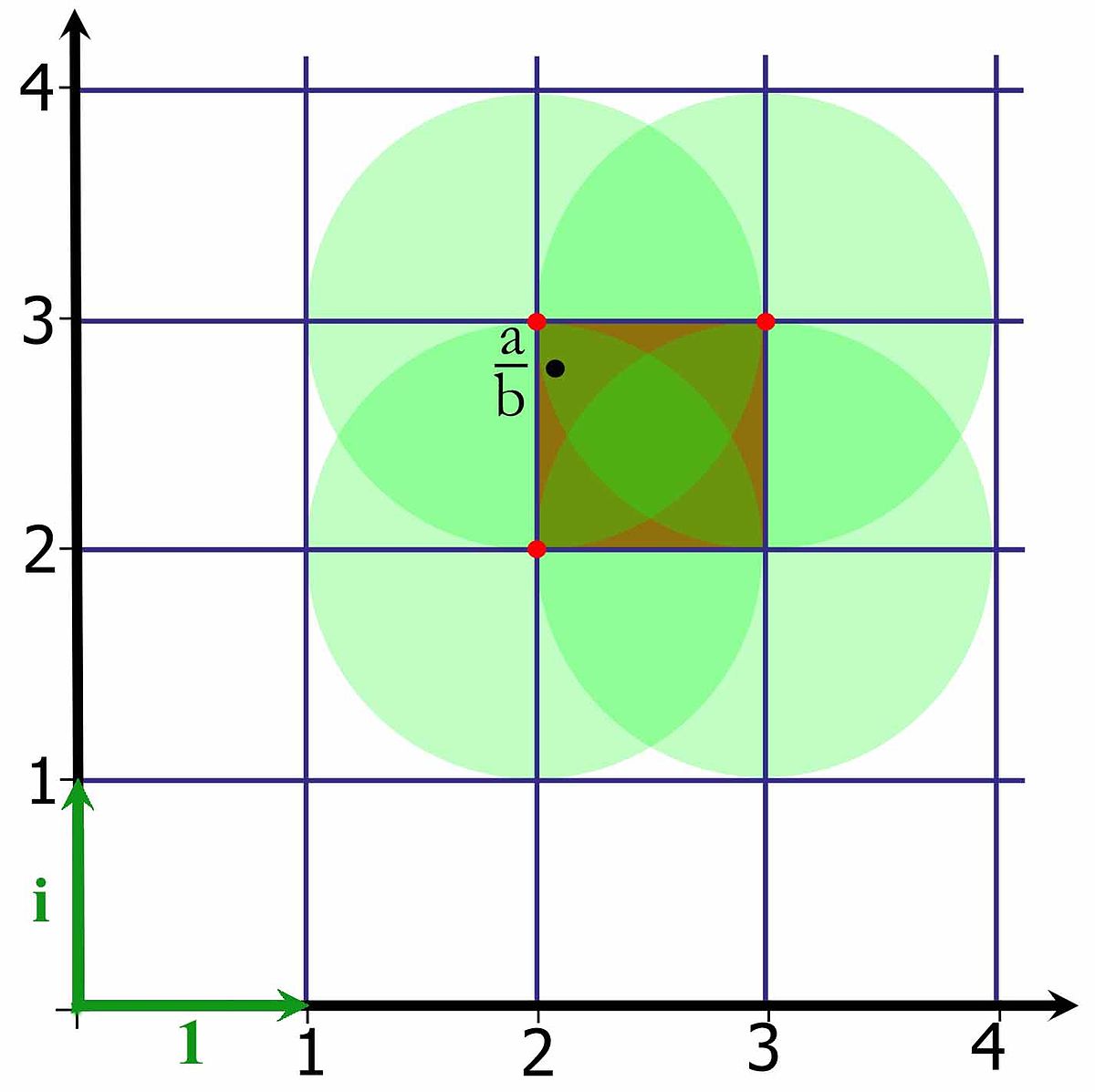
Les entiers de Gauss noté Z[i] correspondent aux nombres de la forme u + i.v ou u et v sont choisis entiers. Ils forment un anneau euclidien, la définition est donnée par la proposition suivante, si N(x) désigne la norme algébrique c’est-à-dire le carré du module de x :
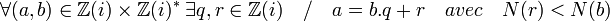
L'application qui à un entier associe sa norme algébrique est bien une application des entiers de Gauss dans un ensemble ordonné, à savoir celui des entiers positifs. Cette norme correspond graphiquement au carré de la distance entre l'origine et l'entier de Gauss.
Dire que la division euclidienne existe signifie que qu'il existe un entier de Gauss à une distance inférieure à 1 du nombre complexe a/b. La figure ci-jointe illustre par un fond rouge le carré de sommet des entiers de Gauss et contenant a/b. La figure montre qu'il existe toujours au moins un entier à une distance inférieure à 1 de a/b. Dans le cas illustré, il en existe trois vérifiant cette propriété. L'unicité de la solution n'est pas une condition nécessaire à l'existence d'une division euclidienne.
Une fois encore, la division euclidienne apporte une arithmétique analogue aux deux cas précédents.
Les applications sont nombreuses. Dedekind a, par exemple, trouvé une preuve élégante du théorème des deux carrés de Fermat à partir de cet ensemble. Certaines équations diophantiennes quadratiques se résolvent bien dans cet ensemble. Gauss a utilisé cette arithmétique pour démontrer la loi de réciprocité quadratique.
En règle générale, un ensemble de cette nature, appelé anneau d'entiers quadratiques, n'a pas de division euclidienne. Ainsi, Z[i√3] n'est pas euclidien.
Autres anneaux euclidiens
- Il existe d'autres anneaux entiers quadratiques euclidiens. Ceux qui ne sont pas inclus dans R sont tous connus. Les autres, comme par exemple celui des entiers de Q(√5), sont dit totalement réels. (Appliquées à des corps quadratiques, les notions de réel et de totalement réel sont équivalentes.) Il est conjecturé qu'il existe une infinité d'anneaux quadratiques totalement réels euclidiens.
- Si K est un corps commutatif, K[[X]] l'anneau de ses séries formelles est aussi euclidien pour la valuation: v(P) = plus petit degré de X dans P.
- Si A est un anneau euclidien et si S est une partie de A stable pour la multiplication. La localisation de A par rapport à S est aussi un anneau euclidien.