Axiome de l'infini - Définition

Introduction

En mathématiques dans le domaine de la théorie des ensembles, l'axiome de l'infini désigne l'un des axiomes de la théorie des ensembles de Zermelo-Fraenkel qui assure l'existence d'un ensemble infini, plus précisément d'un ensemble qui contient une représentation des entiers naturels. Il apparait dans la première axiomatisation de la théorie des ensembles, publiée par Ernst Zermelo en 1908, sous une forme cependant un peu différente de celle exposée ci-dessous.

Énoncé de l'axiome

Il existe plusieurs variantes de l'axiome, suivant par exemple que l'on dispose de la notion d'ordinal ou non. Une façon très intuitive serait de dire qu'un ensemble qui représente celui des entiers naturels existe. En fait on a juste besoin de montrer qu'un ensemble ayant pour éléments des représentations des entiers naturels (et éventuellement d'autres) existe. Pour représenter les entiers naturels on utilise un 0 et une opération successeur. Suivant les idées de von Neumann, on va représenter 0 par l'ensemble vide (qui a 0 éléments) et le successeur par la fonction x → x ∪ {x}, qui à un ensemble associe celui obtenu en ajoutant l'ensemble de départ comme élément (et qui vérifie intuitivement que si x a n éléments, alors x ∪ {x} en a n +1). L'existence de l'ensemble vide est assurée par un axiome ad hoc, ou par d'autres axiomes de la théorie. Pour un ensemble x donné, on peut former le singleton {x} par l'axiome de la paire, et la réunion x ∪ {x} par l'axiome de la réunion et à nouveau l'axiome de la paire.

On a évidemment que le successeur de tout ensemble est non vide : pour tout ensemble x, x ∪ {x} ≠ ∅. On montrera ensuite que, sur les entiers au moins, la fonction successeur est bien injective, ce qui assurera, avec la précédente propriété, qu'un ensemble qui contient 0 et le successeur de chacun de ses éléments contient bien une copie des entiers, et donc est infini au sens intuitif. On prendra d'ailleurs cette représentation comme définition des entiers en théorie des ensembles.

L'axiome s'écrit donc :

Il existe un ensemble auquel appartient l'ensemble vide et qui est clos par application du successeur x → x ∪ {x},

c'est-à-dire dans le langage formel de la théorie des ensembles :

à noter que est juste une abréviation pour par exemple , et que est une abréviation pour c'est-à-dire que l'axiome s'énonce bien dans le langage de la théorie des ensembles : le calcul des prédicats du premier ordre égalitaire avec pour seul symbole non logique celui pour l'appartenance, « ∈ » .

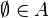
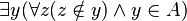
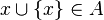
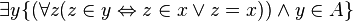
Variantes

Il existe plusieurs variantes pour l'énoncé de l'axiome. Celle donnée au-dessus fait directement référence à la construction la plus usuelle des entiers en théorie des ensembles et se développe naturellement dans la théorie de Zermelo (on n'a jamais eu besoin du schéma d'axiomes de remplacement). Cependant il existe d'autres énoncés de l'axiome avec des variations plus ou moins importantes.

Ordinaux

Les ordinaux de la théorie des ensembles sont définis comme les ensembles transitifs (strictement) bien ordonnés par l'appartenance. 0n a vraiment défini ainsi les ordinaux au sens intuitif (tout bon ordre est isomorphe à un et un seul ordinal) en présence du schéma de remplacement (utile pour l'existence), donc dans la théorie de Zermelo-Fraenkel (ZF). Cela dit cette définition ne pose aucun problème en elle-même dans la théorie de Zermelo (sans axiome de l'infini).

Il est à peu près immédiat que la classe des ordinaux est stable par l'opération successeur introduite sur les entiers : si α est un ordinal α ∪ {α} est un ordinal. Un ordinal est dit limite s'il est non vide et n'est le successeur d'aucun ordinal. On remarque que l'ensemble vide est un ordinal, ainsi que tous les entiers non nuls définis ci-dessus par passage au successeur, aucun n'est donc un ordinal limite.

Un énoncé possible de l'axiome de l'infini est le suivant :

Il existe un ordinal limite.

Il est équivalent à celui donné ci-dessus. En effet on a montré que ω était un ensemble transitif bien ordonné par l'appartenance, c'est-à-dire un ordinal. D'autre part, par construction, les seuls éléments de ω, c'est-à-dire les seuls ordinaux strictement inférieurs à ω, sont les entiers qui ont tous pour successeur un entier, donc ω est un ordinal limite.

Réciproquement on montre qu'un ordinal limite est nécessairement un sur-ensemble de ω. En effet un tel ordinal α a forcément l'ensemble vide pour élément, puisque son plus petit élément β (qui existe car α est non vide par définition) en est aussi un sous-ensemble par transitivité, et s'il n'était pas vide on aurait un élément de α strictement plus petit que β. D'autre part si γ appartient à α son successeur aussi. En effet son successeur γ ∪ {γ} est par transitivité un sous-ensemble de α, qui ne peut être α car celui-ci est limite, et qui est un ordinal. Il existe donc des éléments de α qui n'appartiennent pas à γ ∪ {γ} et donc auxquels γ appartient par totalité de l'ordre sur α. Le plus petit d'entre eux est la borne supérieure de l'ensemble γ ∪ {γ} pour l'appartenance dans α ; il ne peut avoir pour élément un ordinal de α qui n'appartienne pas à γ ∪ {γ} : on aurait trouvé un plus petit majorant de γ ∪ {γ} par totalité de l'ordre dans α. C'est donc γ ∪ {γ} lui-même, qui appartient alors à α.

Les deux énoncés sont donc équivalents, modulo les autres axiomes de la théorie des ensembles (ceux de Zermelo suffisent).

Version de Zermelo

La version de Zermelo de l'axiome de l'infini est qu'il existe un ensemble auquel appartient l'ensemble vide, et tel que, si x appartient à cet ensemble, alors le singleton {x} y appartient également.