Cladistique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La cladistique, du grec ancien κλάδος (klados) signifiant « branche », aussi appelée systématique phylogénétique, est une théorie concernant la classification phylogénétique, qui est l'étude de la classification des êtres vivants selon leurs relations de parenté, dans un cadre évolutionniste. Elle repose sur la construction de groupes monophylétiques (ou clades), c'est-à-dire des groupes incluant un ancêtre et l'ensemble de sa descendance.
Description générale
La cladistique se distingue des autres domaines de la systématique car elle cherche à établir les relations de parenté strictes entre les taxons en distinguant caractères dérivés (apomorphies) et primitifs (plésiomorphies). Un groupe monophylétique ne se fondera que sur le partage de caractères dérivés propres, également appelés synapomorphies.
Cette méthode de reconstruction phylogénétique a été introduite dans les années 1950 par l'entomologiste allemand Willi Hennig.
Les résultats de ce type de reconstruction peuvent être représentés sous forme de graphes connexes non cycliques, ou arbres, appelés ici cladogrammes. Ces arbres récapitulent ainsi les relations de parenté entre les taxons considérés. Les données morphologiques, moléculaires et comportementales sont utilisées dans les travaux cladistiques. La reconstruction d'arbres est largement assistée par des logiciels informatiques.
Lecture d'un cladogramme
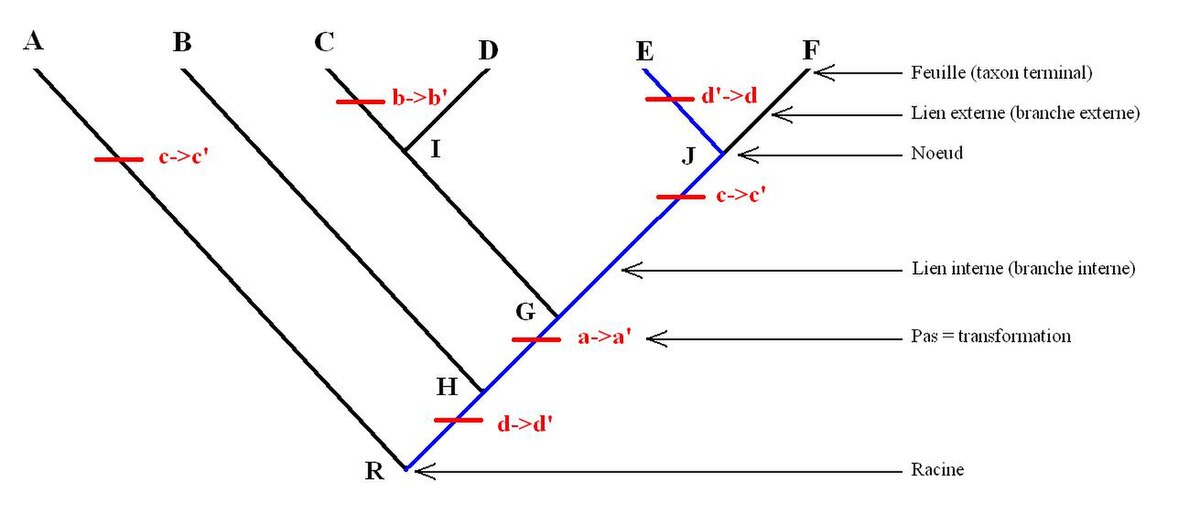
En général les possessions de caractères sont résumées dans un tableau appelé matrice taxons/caractères donnant pour chaque caractère de chaque taxon son état. Ici nous allons utiliser un exemple hypothétique. Par convention, pour chaque caractère "x", l'état primitif est noté x et l'état dérivé x' (ça aurait pu être l'inverse). Tous les caractères en x sont donc plésiomorphes (exemple b) et les caractères en x' son apomorphes (exemple b'). Voici la matrice hypothétique:
| caractère | taxon A | taxon B | taxon C | taxon D | taxon E | taxon F |
|---|---|---|---|---|---|---|
| Caractère "a" | a | a | a' | a' | a' | a' |
| Caractère "b" | b | b | b | b | b' | b |
| Caractère "c" | c' | c | c | c | c' | c' |
| Caractère "d" | d | d' | d' | d' | d | d' |
| Caractère "e" | e | e | e | e | e | e |
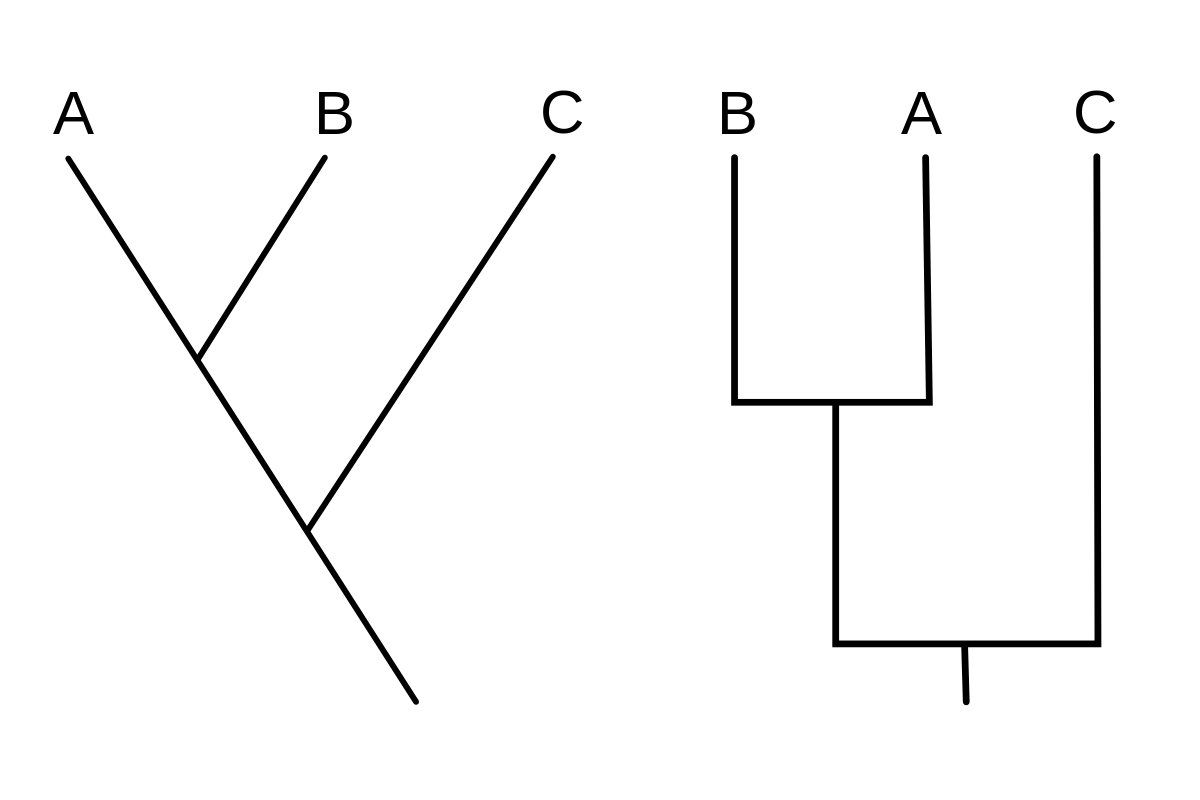
On considère l'arbre suivant pour les taxons A, B, C, D, E et F: (A(B((C, D)(E, F)))). Cet arbre est choisit arbitrairement. Ici R=A+B+C+D+E+F: c'est la racine ou le nœud qui contient tout. H=B+C+D+E+F G=C+D+E+F I=C+D et J=E+F, donc G=I+J. Les taxons H, G, I et J sont des nœuds internes (Ce sont des taxons au même titre qu'A, B, C etc.). L'ordre dans lequel les taxons sont disposés ne change pas la lecture de l'arbre. En effet l'arbre (A(B((C, D)(E, F)))) est équivalent à l'arbre ((B((D, C)(E, F)))A)par exemple.
La position la plus parcimonieuse des caractères (en minimisant le nombre de fois où ils apparaissent) est représentée dans l'image associée par des barres rouges où x→x' indique le passage de l'état x à x' et x'→x le passage de l'état x' à l'état x. Les barres rouges représentent des transformations sur l'arbre ou "pas évolutifs".
Selon la disposition la plus parcimonieuse des caractères, le caractère a' est commun à C, D, E, et F, c'est donc une synapomorphie de G.
Le caractère b' n'apparaît que pour un seul taxon terminal : C. C'est donc une autapomorphie de C, c'est-à-dire un caractère dérivé du taxon C uniquement, qui ne nous renseigne pas sur ses relations de parentés avec les autres taxons.
Le caractère "e" reste à l'état e pour tous les taxons, c'est donc une symplésiomorphie de R. Les caractères "c" et "d" subissent deux transformations (deux pas) dans l'arbre, ce sont donc des homoplasies.
Sur la ligne bleue (allant de la racine à E), le caractère "d" est impliqué deux fois sous l'état de caractère d, c'est donc une réversion. Pour le caractère "d" on a alors la morphocline, ou suite de transformations suivante : d→d'→d. L'état de caractère d possédé par E n'est donc pas réellement primitif mais semblable à l'état primitif.
Le caractère "c" apparaît dans deux morphoclines différentes sous l'état c', c'est donc une convergence. Les deux états de "c" pour A et J ne sont donc pas des homologies secondaires : ce n'est pas le même caractère hérité d'un ancêtre commun.
Sur cet arbre on peut compter le nombre de transformations, il y en a 6. On compte donc 6 pas.
Deux groupes frères sont les groupes les plus apparentés entre eux qu'ils ne le sont de n'importe quel autre. Ici par exemple C est groupe frère de D, B groupe frère de G, J groupe frère de I, etc.
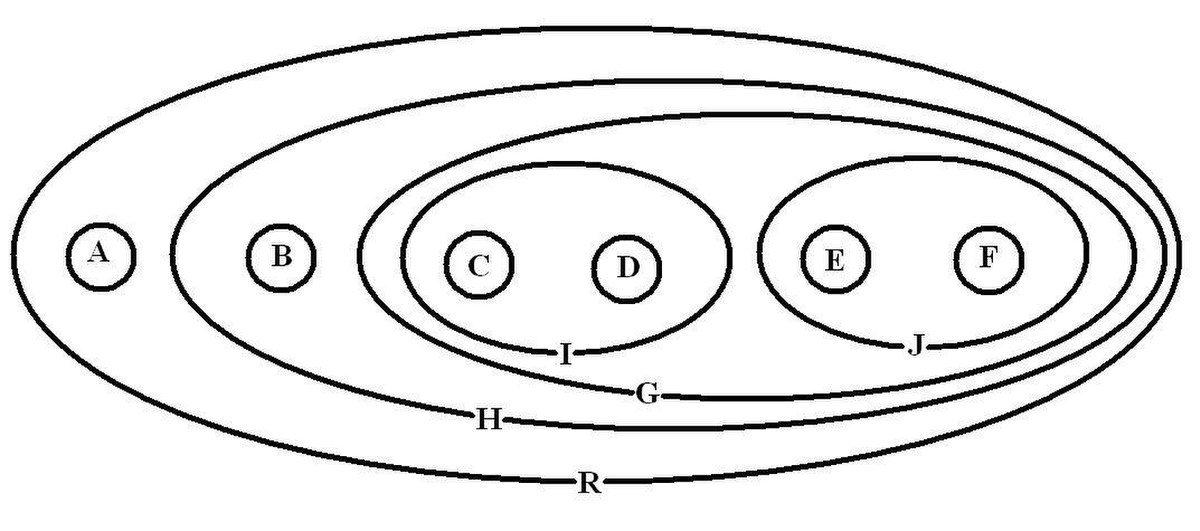
Un cladogramme représente une hiérarchie, au sens mathématique du terme, c'est à dire un ensemble de classes strictement incluses les unes dans les autres. En effet, ici C et D appartiennent à I et tous les groupes appartiennent à R (R étant la racine donc la classe comprenant tout). Un cladogramme peut donc être représenté en diagramme de Venn. L'image ci-dessous représente le cladogramme utilisé dans l'exemple sous forme de diagramme de Venn.