Code linéaire - Définition

Définitions

• Soit p un nombre premier, d une puissance de p, n un entier strictement positif et k un entier plus petit que n. Un code linéaire C de dimension k et de longueur n est un sous-espace vectoriel de F_dⁿ de dimension k. Si d est égal à deux, le code est dit binaire. Sinon, on parle de code linéaire de base d.

Ici, F_d désigne l'unique corps à d éléments (cf l'article corps fini). On remarque que l'espace vectoriel des suites à valeurs dans F_d est identifié à F_dⁿ. L'espace vectoriel F_dⁿ est muni de la distance de Hamming.

Comme pour les autres codes correcteurs, la notion de paramètres s'applique. Cependant, pour tenir compte de la structure d'espace vectoriel, elle est un peu modifiée:

• Les paramètres d'un code sont notés [n, k, δ] ou δ désigne la distance minimale entre deux points du code.

La définition de paramètre pour les codes linéaires n'est donc pas compatible avec celle, plus générique utilisées pour les codes correcteurs. Pour cette raison, traditionnellement les paramètres d'un code linéaire sont notés [n, k, δ] et ceux d'un code correcteur général {n, M, δ}.

Comme précédemment, il existe une application d'encodage : φ.

• L'application d'encodage φ d'un code linéaire est une application linéaire injective de F_d^k dans F_dⁿ.

• La matrice G de F_dⁿ dans les bases canoniques est dite matrice génératrice du code C. Elle vérifie l'égalité suivante:

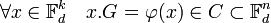
Le contrôle permettant la vérification et les éventuelles corrections est donné par une application linéaire h de F_dⁿ dans F_d^n-k ayant pour noyau C. La théorie de l'algèbre linéaire montre qu'une telle application existe, il suffit par exemple de considérer un projecteur sur un sous-espace supplémentaire de C parallèlement à C.

• La matrice H de h dans les bases canoniques est dite matrice de contrôle du code C. Elle vérifie les propriétés suivantes:

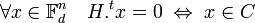
Le terme de matrice de parité est aussi utilisé pour désigner la matrice de contrôle.

Remarque : Ces notations sont utilisées dans le reste de l'article.

Traitement des erreurs

Détection

La technique la plus simple de traitement des erreurs se limite à une validation. Si le message n'est pas élément du code, alors il est déclaré faux. En général, une nouvelle demande de transmission est la technique de correction.

La méthode la plus fréquemment utilisée consiste à adjoindre au message un ou plusieurs bits de contrôle correspondant à la somme dans le corps fini des coefficients du message. Cette technique est l'analogue de la preuve par neuf.

Quitte à augmenter le nombre de bits de contrôle, cette méthode peut accroitre son niveau de fiabilité. Si la probabilité est suffisamment forte pour supposer qu'une seule erreur est à même de se glisser dans le message, alors un bit de contrôle remplit la condition.

Dans le cas d'un unique bit de contrôle, alors les paramètres du code sont [n, n - 1, 2]. Un tel code ne peut pas procéder à la correction de l'erreur par lui-même. En effet pour chaque erreurs, il existe n - 1 points du code qui sont proches. Des informations supplémentaires sont nécessaires pour une auto-correction.

L'implémentation est simple, le calcul de l'image du message par la matrice de contrôle fournit l'information. Si l'image est nulle alors le message correspond à un code et il est sans erreur, sinon une erreur est déclarée.

Correction

La question est ici traitée uniquement dans le cas des codes systématiques. Non seulement c'est la solution considérée par l'industrie, mais de plus, toute autre configuration est équivalente à celle-là.

Dans un premier temps, il est possible de considérer uniquement le problème au vecteur nul. Le message reçu possède donc comme k premières coordonnées 0 et des bits de contrôle c non tous nuls. Cette situation correspond à une erreur, car l'image du vecteur nul par la matrice génératrice donne le vecteur nul et donc les bits de contrôle sont tous nuls pour un code ayant ses k premières coordonnées nulles.

La correction correspond au message m de plus petit poids de Hamming et ayant pour image par la matrice de contrôle -H.c. Si le nombre d'altérations ayant généré le vecteur (0, c) est inférieur à (δ - 1)/2, alors il existe un unique m tel que H.m = -H.c. Ici, H.c désigne par abus le vecteur H.(0,c). Le code associé est m - c et le message initial est m. On vérifie de fait que H.(m - c) = 0 et m - c est un code. Il est alors possible, à chaque valeur de H.c, d'associer une correction m.

• La valeur H.(0,c) où H est une matrice de contrôle systématique et c un ensemble de bits de contrôle non nuls est appelée un syndrome.

Dans le cas général, si l est un message reçu qui n'est pas élément du code, son image par la matrice de contrôle est une valeur correspondant à un H.c donné. Il apparait que m est la plus petite correction à appliquer à l pour obtenir un code. En effet, H(l + m) est égal à H.c - H.c et la minimalité est une conséquence du paragraphe précédent.

La détermination de la valeur m pour un H.c dépend largement du choix du code. Il correspond au problème classique couvert par la programmation linéaire. Dans la pratique, il est rare que de telles méthodes soient employées. Soit les bits de contrôles sont en nombre réduits, et la combinatoire est réduite, soit l'espace est vaste et le code dispose d'autres propriétés souvent polynomiales et décrite dans l'article code cyclique.

L'implémentation, dans la mesure où l'espace des bits de contrôle est réduit est en général réalisée par une table de hachage. Cette table établit une bijection entre chaque syndrome et le message de poids minimal ayant pour image par la matrice de contrôle le syndrome.

• Une implémentation de la correction à l'aide d'une table de hachage fournissant une bijection entre les syndromes et les messages de poids minimal est appelée un décodage par syndrome.