Code linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Toutes les propriétés de l'algèbre linéaire s'appliquent aux codes linéaires. Le code est ainsi à la fois plus facile à implémenter et à décoder. De plus les outils de génération d'espace vectoriel comme l'espace dual ou le produit tensoriel permettent de concevoir des nouveaux codes, parfois plus adaptés aux contraintes industrielles.
Matrice génératrice
L'application d'encodage est linéaire, elle se représente donc et se calcule grâce à sa matrice génératrice. Un code est entièrement défini par sa matrice génératrice, de dimension nxk. De plus comme les propriétés de son code ne dépendent que de la géométrie φ(E). Si f est un isomorphisme de E, le code défini par l'application φof est le même que celui de φ. Ce qui donne lieu à la définition suivante :
-
- Deux codes sur un même alphabet Fd de longueur k définis par deux matrices génératrices G et G' tel qu'il existe une matrice carrée inversible P d'ordre k vérifiant G =G'.P sont dits équivalents.
Il existe une forme particulièrement simple pour la matrice G :
-
- Un code linéaire dont la matrice génératrice possède pour k premières lignes une matrice identité d'ordre k est dit code systématique.
L'article associé à ce paragraphe démontre une propriété importante :
-
- Tout code linéaire est équivalent à un code systématique.
Cette écriture accélère et simplifie l'encodage et le décodage. La matrice prend alors la forme suivante :
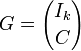
Les coordonnées de la matrice C correspondent à la redondance, leur objectif est la détection et la correction d'erreurs éventuelles:
-
- Les n - k dernières coordonnées d'un mot du code systématique sont dites bits de contrôle ou parfois somme de contrôle.
Matrice de contrôle
Dans le cas linéaire, le code est un sous-espace vectoriel de dimension k. Il existe alors une application linéaire surjective de F dans un espace de dimension n - k ayant pour noyau exactement le code :
-
- Une matrice de contrôle d'un code φ(E) est une matrice H de dimension nxn - k tel que :
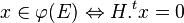
Dans le cas d'un code systématique, l'expression de la matrice génératrice offre immédiatement celle d'une matrice de contrôle.
-
- Dans le cas d'un code systématique, si G est l'expression d'une matrice génératrice alors l'expression suivante est celle d'une matrice de contrôle :
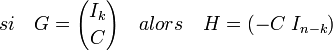
Ici, Ik désigne la matrice carrée identité d'ordre k. Cette matrice offre une manière relativement simple de calculer la distance minimale :
-
- La distance minimale δ d'un code linéaire est égale à la dimension du plus petit sous-espace vectoriel S de F généré par des éléments de la base canonique et tel que la restriction de la matrice de contrôle à S soit non injective.
Distance de Hamming
Dans le cas d'un code linéaire, la distance de Hamming s'exprime comme une distance issue d'une pseudo-norme. Le poids de Hamming, qui à un code associe le nombre de coordonnées non nulles, joue ici le rôle de pseudo-norme.
-
- Si ω désigne le poids de Hamming pour un code linéaire C, alors la distance de Hamming d est définie par la formule suivante:
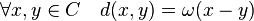
La linéarité de la structure sous-jacente introduit une propriété directe:
-
- La distance minimale δ entre deux points du code est égale au minimum du poids des mots du code non nuls.
Pour s'en convaincre, il suffit de remarquer que si x et y sont deux mots du code, alors leur différence est aussi un mot du code.
Borne de Singleton et code MDS
Le nombre maximum d'erreurs assurément corrigibles t découle directement de la distance minimale δ. En effet, t est le plus grand entier strictement inférieur à δ/2. La situation idéale est celle où les boules fermées de centre les mots du code et de rayon t forment une partition de F. On parle alors de parfait.
-
- La majoration suivante est vérifiée pour tous les codes linéaires. Elle se nomme borne de Singleton:
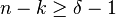
Si la borne de Singleton est atteinte, le code est dit MDS.
Code dual
La structure linéaire du code donne naturellement naissance à la notion de code dual. Si l'espace vectoriel contenant C est muni d'une structure dual à l'aide du produit scalaire canonique, alors le code C possède naturellement un espace vectoriel dual supplémentaire.
-
- Le code dual d'un code linéaire C est le sous-espace supplémentaire orthogonal à C si l'espace est muni du produit scalaire canonique. C'est un code de même longueur et de dimension n - k. Il est souvent noté
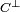
- Le code dual d'un code linéaire C est le sous-espace supplémentaire orthogonal à C si l'espace est muni du produit scalaire canonique. C'est un code de même longueur et de dimension n - k. Il est souvent noté
Dans le cas d'un code systématique, cas où il est toujours possible de se ramener, la matrice de contrôle de C devient une matrice génératrice de son dual. Il suffit alors de réordonnancer la base pour obtenir un code systématique. De même une matrice génératrice de C est une matrice de contrôle de son dual.
Il est possible de calculer la distance minimale de
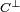
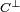
Code produit
L'algèbre linéaire offre de multiples autres techniques compatibles avec les codes. Le produit tensoriel est un exemple. À deux espaces vectoriels, il en associe un troisième isomorphe aux applications linéaires du premier espace dans le deuxième.
-
- Si C0 (resp. C1) est un code linéaire de paramètre [n0, k0, d0] (resp. [n1, k1, δ1]), alors le produit tensoriel des deux codes est un code de paramètre [n0.n1, k0.k1, δ0.δ1]. Ce code est appelé code produit de C0 et C1.
Il permet de corriger toute configuration comportant moins de δ0.δ1/4 erreurs.

















































