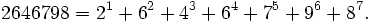Coïncidence mathématique - Définition

Autres curiosités numériques

• .
• , où φ est le nombre d'or (une égalité étonnante avec un angle exprimé en degrés) Voir Nombre de la bête.
• et sont les seuls carrés et cubes séparés de 2 unités.
• .
• est l'unique solution entière de (voir fonction W de Lambert pour une preuve formelle).
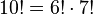
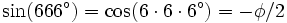
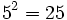
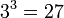
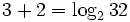
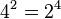
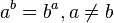
• Non seulement , mais aussi .
• est égal au nombre plastique ψ (solution de ψ³ = 1 + ψ) à 0.111% près.
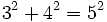
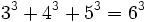
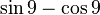
• 31, 331, 3331 etc. jusqu'à 33333331 sont tous des nombres premiers, mais pas 333333331.
• Le nombre de Fibonacci F₂₉₆₁₈₂ est (probablement) un nombre semi-premier, puisque F₂₉₆₁₈₂ = F₁₄₈₀₉₁ × L₁₄₈₀₉₁ où F₁₄₈₀₉₁ (30949 chiffres) et le nombre de Lucas L₁₄₈₀₉₁ (30950 chiffres) sont simultanément nombres premiers probables.
• Dans le paradoxe des anniversaires, le nombre intervient ; Richard Arriata note qu'il est « étrangement » égal à ln(2) sur 4 chiffres.

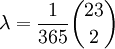
Coïncidences sur les unités

• π secondes est un nanosiècle (c'est-à-dire 10 ^{− 7} années); vrai à 0,5% près.
• un attoparsec par microfortnight (1 fortnight = 14 jours) est approximativement 1 pouce par seconde (en réalité 1,0043 pouces par seconde).
• un furlong par fortnight est approximativement égal à 1 centimètre par minute.
• un attoparsec cubique (un cube d'un attoparsec de côté) est à 1% près égal à 1 once liquide américaine.
• un mille international (mile) est environ φ kilomètres (vrai à 0,5% près), où est le nombre d'or. Puisque φ est la limite du ratio de 2 termes consécutifs de la suite de Fibonacci, cela donne une suite d'approximations de correspondances entre miles et kilomètres : F_n mi = F_{n + 1} km, par exemple 5 mi = 8 km, 8 mi = 13 km.
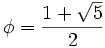
• Une autre bonne approximation est : 1 mile = ln(5) km. En effet, 1 mile = 1,609344 km et ln(5) = 1,6094379124341...
• N_A ≈ 2⁷⁹, où N_A est le nombre d'Avogadro; vrai à environ 0,4% près. Cela signifie qu'1 yobibyte est approximativement un peu plus du double d'une mole de bytes. Ceci signifie également qu'1 mole de matière (c'est-à-dire 12 g de carbone), ou 25 l de gaz à température et pression normales, ne peuvent pas être divisés en 2 plus de 79 fois.
• La vitesse de la lumière dans le vide est d'environ un pied par nanoseconde (vrai à 2% près), ou encore 3×10⁸ m/s (vrai à 0,07% près), ou enfin 1 milliard de km/h (vrai à 7,93% près)

Coïncidences décimales

• .
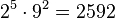
• 1! + 4! + 5! = 145.
• ,     ,    
• et .
•  ;  ;  ;
• .
• (important dans le symbolisme numérique de la cathédrale Saint-Étienne de Vienne)
• .
• et , qui arrondi à 8 chiffres fait 0,05882353
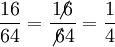
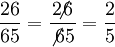
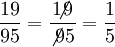
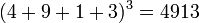
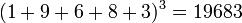
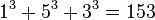
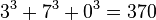
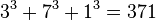
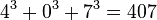
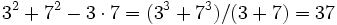
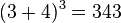
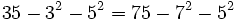
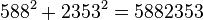
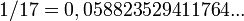
• Un nombre (parmi d'autres) qui égale la somme de ses chiffres aux puissances consécutives :