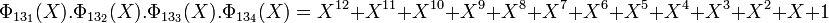Corps fini - Définition

Polynôme irréductible

Extension normale et polynôme cyclotomique

Soit p un nombre premier n un entier strictement positif et K un corps de cardinal q = pⁿ.

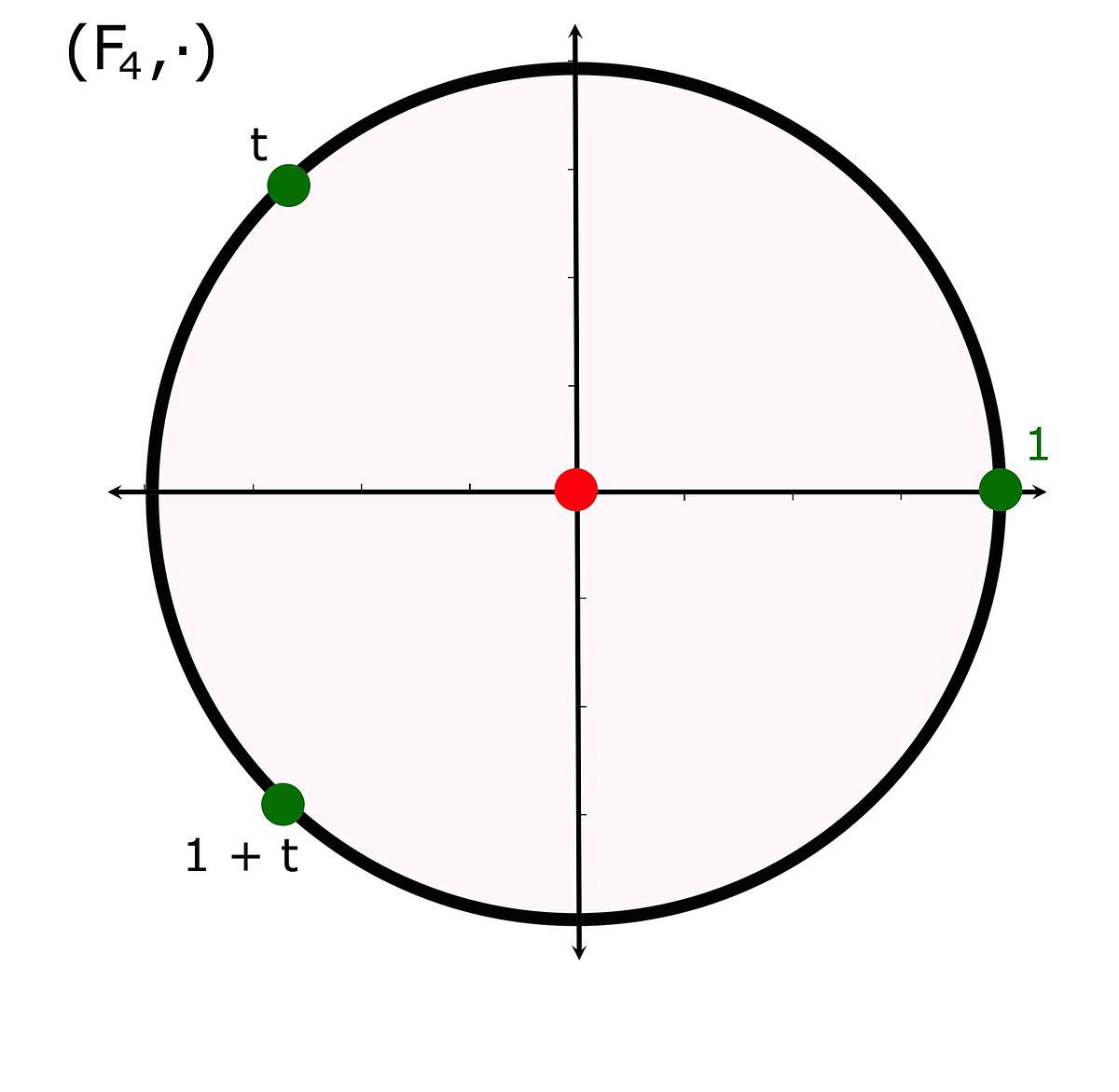
Le paragraphe précédent montre que tout élément de K est racine du polynôme X^q - X. À l'exception de l'élément nul, tout élément est racine de l'unité. Cette propriété est illustrée sur la figure de droite, les trois éléments non nuls de F₄ sont les trois racines de l'unité. Cette remarque amène la proposition suivante:

• Tout élément de K^* est racine de l'unité et tout polynôme irréductible autre que X divise un polynôme cyclotomique.

Si φ désigne la fonction indicatrice d'Euler il existe exactement φ(q - 1) éléments primitifs dans K. Chaque élément primitif possède un polynôme minimal à coefficients dans F_p de degré n égal à la dimension de K considéré comme espace vectoriel sur F_p.

• Le nombre N_m de polynômes irréductibles unitaires de degré m à coefficients dans K est égal à, si μ désigne la fonction de Möbius :

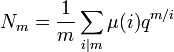
La démonstration est proposée dans l'article Fonction de Möbius.

• Il existe exactement φ(q - 1) éléments primitifs dans K, correspondant à φ(q - 1)/n polynômes sur F_p.

Cependant, il peut y avoir d'autres polynômes irréductibles de même degré: dans F₉, on a x⁸ - 1 = (x - 1)(x + 1)(x² + 1)(x² + x +2)(x² + 2x + 2), x² + 1, bien qu'irréductible, n'étant le polynôme minimal d'aucun des 4 éléments primitifs.

Cette propriété est associée à une définition dans la théorie des corps finis:

• Deux éléments de K sont dits conjugués si et seulement s'ils possèdent le même polynôme irréductible. La relation de conjugaison est une relation d'équivalence. Chaque classe possède comme cardinal le degré du polynôme irréductible associé.

Deux propriétés supplémentaires indiquent la relation entre les polynômes cyclotomiques et leur degré dans le cas de la caractéristique p. Elles sont démontrées dans l'article associé.

• Un diviseur du polynôme cyclotomique d'indice q - 1 sur F_p est de degré l'ordre multiplicatif de p modulo q - 1.

• Le produit des polynômes irréductibles de degré n est le polynôme cyclotomique d'indice q - 1.

Caractéristique deux

Il existe exactement deux polynômes unitaires de degré un et le deuxième est le polynôme cyclotomique d'indice un:

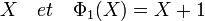
Il existe exactement un polynôme de degré deux irréductible, il est primitif, c'est le polynôme cyclotomique d'indice trois. Il est scindé dans F₄ et l'on reconnaît le polynôme cyclotomique d'indice 3 dans Z:

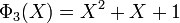
Il existe exactement deux polynômes de degré trois irréductibles car le corps contient six éléments hors de son unique sous-corps. Le groupe multiplicatif contient sept éléments, donc six sont générateurs. Il existe donc deux polynômes primitifs ce sont les deux polynômes cyclotomiques d'indice sept, scindé dans F₈:

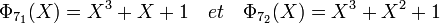
Leur produit est bien l'image du polynôme cyclotomique à coefficients dans Z:

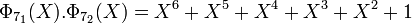
Le corps F₁₆ contient deux sous-corps F₄ et F₂. En conséquence, il existe exactement trois polynômes irréductibles de degré quatre. Le groupe multiplicatif F₁₆^* contient huit générateurs car l'indicatrice d'Euler appliqué à quinze est égal à huit, il existe donc deux polynômes de racines des éléments primitifs. Le polynôme restant est celui correspondant au polynôme cyclotomique d'indice cinq. Il existe donc deux polynômes cyclotomiques d'indice quinze et un polynôme cyclotomique d'indice cinq.

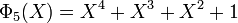
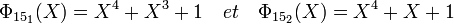
Une fois encore, le produit des deux polynômes cyclotomiques d'indice 15 est bien l'image du polynôme cyclotomique à coefficients dans Z:

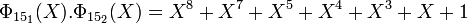
Caractéristique trois

Il existe trois polynômes unitaires de degré un, le deuxième est le polynôme cyclotomique d'indice un et le troisième d'indice deux.

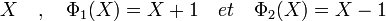
L'extension d'ordre neuf contient six éléments hors du corps premier, elle est de dimension deux, il existe donc exactement trois polynômes irréductibles. Le groupe multiplicatif est d'ordre huit et contient quatre éléments générateurs, deux des polynômes sont donc cyclotomiques d'ordre huit, le dernier est cyclotomique d'ordre quatre.

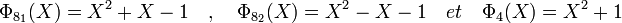
L'extension d'ordre vingt-sept contient un unique sous-corps le corps premier. Il existe donc vingt-quatre éléments hors de tout sous-corps et huit polynômes irréductibles de degré trois. Le groupe multiplicatif contient vingt-six éléments et douze générateurs et il existe quatre polynômes cyclotomiques d'indice vingt-six et quatre d'indice treize.

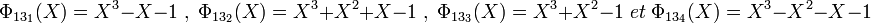
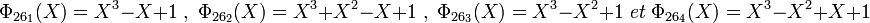
On vérifie de même que :