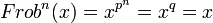Corps fini - Définition

Extensions de corps finis

On montre d'abord que tout corps fini est de cardinal la puissance d'un nombre premier, puis qu'il existe à isomorphisme près un unique corps fini de tel cardinal donné.

Caractéristique et cardinal

Soit K un corps fini et p sa caractéristique, c'est-à-dire le plus petit entier tel que l'addition de 1 itérée p fois soit égal à 0. Un tel nombre existe car sinon, le groupe additif engendré par 1 serait infini et K ne contient pas de sous-ensemble infini. De plus, p est un nombre premier. En effet, si a et b sont des entiers tels que a.b = p, alors le produit de a par b est nul dans K, ce qui montre que soit a soit b est un multiple de p, car il n'existe pas de diviseur de 0 dans un corps. L'unique homomorphisme d'anneaux unitaires de Z dans K induit une injection de Z/p.Z dans K son image est le sous-corps de K formé des éléments du sous-groupe additif engendré par 1. C'est un sous-corps de K contenant p éléments et isomorphe à Z/ pZ, encore noté F_p.

Le corps K hérite donc d'une structure d'espace vectoriel sur F_p. Sa dimension étant nécessairement finie, notons la n, son cardinal est alors pⁿ. Pour résumer :

• Le cardinal d'un corps fini est une puissance d'un nombre premier qui en est sa caractéristique. Plus exactement, tout corps fini est une extension finie d'un corps premier F_p.

Automorphisme de Frobenius

On suppose ici donné un corps K fini de caractéristique p, de cardinal q = p^k. On peut alors montrer la formule importante suivante :

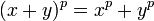
L'application qui, à x, associe x^p de K dans lui-même est un endomorphisme bijectif, appelé endomorphisme de Frobenius et est noté ici Frob. Cet automorphisme est important dans l'étude des corps finis. On trouvera le théorème suivant démontré dans l'article dédié :

• Tout corps fini est parfait, c'est-à-dire que ses extensions algébriques sont séparables.

Ce fait a une conséquence importante, par le théorème de l'élément primitif, qui affirme que toute extension finie et séparable est simple c’est-à-dire engendrée par un unique élément :

• Toute extension algébrique de corps finis est simple.

L'étude de l'automorphisme de Frobenius permet aussi de déterminer les polynômes irréductibles sur le corps fini K :

• Les polynômes irréductibles de K de degré n sont les diviseurs premiers de degré n du polynôme suivant et sont donc tous cyclotomiques :

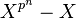
Existence d'un corps fini de cardinal pⁿ

Soit n un entier strictement positif, q l'entier égal à pⁿ et L le corps de décomposition du polynôme P(X) = X^q - X sur le corps F_p. L'ensemble des éléments invariants par l'automorphisme Frobⁿ est une extension K de F_p. K est exactement l'ensemble des racines de P(X). Or P(X) est scindé sur K, il est de plus séparable car premier avec son polynôme dérivé égal à 1 (cette propriété est démontrée dans le paragraphe Cas des polynômes de l'article Extension séparable). K contient donc autant de racines que son degré, c’est-à-dire pⁿ.

Groupe multiplicatif et conséquences

Soit K un corps fini de cardinal q = pⁿ. Alors, le groupe multiplicatif de ce corps est de cardinal q - 1 ; soit e son exposant, c'est un diviseur de q - 1. Il vient alors que le polynôme X^e - 1 à coefficients dans K, possède q - 1 racines distinctes et est de degré e, ce qui implique que e est supérieur à q - 1, puis l'égalité. L'exposant du groupe multiplicatif étant égal à son ordre, et comme dans un groupe fini commutatif l'exposant est toujours l'ordre d'un élément du groupe, on trouve :

• Le groupe multiplicatif d'un corps fini est cyclique.

En conséquence, tout corps de cardinal q est un corps de décomposition du polynôme X^q - X sur F_p. Deux tels corps de décomposition sont isomorphes, donc si on fixe une clôture algébrique de F_p, alors :

• Il existe un et un seul corps de cardinal q, noté F_q, contenu dans la clôture algébrique fixée.

Propriétés galoisiennes

Une conséquence du paragraphe précédent est que le polynôme minimal ψ_q-1(X) d'un élément primitif est de degré n, et le corps F_q de cardinal q est isomorphe au corps de rupture F_p[X]/ψ_q-1(X). Or, ce polynôme est diviseur du polynôme X^q-1-1, qui est scindé dans F_q. Ainsi :

• L'extension F_q/F_p est corps de décomposition du polynôme cyclotomique ψ_q-1(X). C'est une extension galoisienne.

Et, plus précisément, l'endomorphisme de Frobenius Frob est un automorphisme du corps F_q' laissant son sous-corps premier invariant, c'est donc un élément du groupe de Galois. Considérant ensuite un élément x primitif dans F_q, on voit que :

et, par primitivité, n est la plus petite puissance de Frob laissant x fixe. Frob est donc un élément d'ordre au moins n du groupe de Galois, qui est d'ordre le degré n de l'extension :

• L'endomorphisme de Frobenius est un générateur du groupe de Galois Gal ( F_q/F_p), qui est en particulier cyclique d'ordre n.

Le théorème fondamental de la théorie de Galois permet la détermination des sous-corps d'un corps fini. Les sous-groupes du groupe de Galois sont les groupes cycliques d'ordre un diviseur de n, en conséquence :

• Il existe exactement autant de sous-corps que de diviseurs d de n pour une extension de cardinal pⁿ. Les sous-corps K' ont pour cardinal p^d, ce sont des extensions de Galois, et le groupe Gal ( K/K' ) est un groupe cyclique d'ordre n/d.

Clôture algébrique

On connaît par ce qui précède toutes les extensions finies, et donc, par réunion, toutes les extensions algébriques des corps finis. Toute clôture algébrique de peut être vue comme le compositum des .

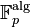
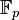
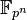
Du point de vue de la théorie de Galois, la famille des groupes , pour n variant, forme donc ce qu'on appelle un système projectif, c'est-à-dire que le groupe de Galois absolu est la limite projective des groupes  ; c'est donc le complété profini de , qui est ainsi un groupe procyclique : un générateur naturel est à nouveau l'endomorphisme de Frobenius, qui peut être vu comme la donnée de la famille compatible des endomorphismes de Frobenius des extensions finies.

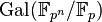
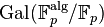
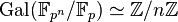
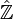
Cette description complète des extensions algébriques des corps finis est un élément important qui intervient dans la théorie des corps de classes pour les corps de nombres et les corps de nombres p-adiques, car leurs corps résiduels sont des corps finis.