Corps fini - Définition

Exemples

Le plus petit corps

Le plus petit corps fini, noté ( , +, . ), ou plus simplement F₂, est composé de deux éléments distincts, à savoir l'élément neutre pour l'addition 0 et l'élément neutre pour la multiplication 1. Voici la définition des opérations « + » et « . » sur ce corps :

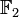
Corps finis complexes

Si p est un nombre premier congru à 3 modulo 4, et a et b des éléments du corps de congruences modulo p, les éléments de type a + i b constituent aussi un corps.

Corps premiers et extensions

Comme Z est un anneau euclidien, a fortiori principal, tout idéal I s'écrit de manière unique sous la forme I = n.Z où n est appelé le générateur positif de I. Par définition, c'est le plus petit entier positif non nul appartenant à I. Les seules structures quotients obtenues à partir de Z sont donc les anneaux commutatifs unitaires Z/n.Z.

Ces anneaux donnent les premiers exemples de corps finis :

• L'anneau Z/nZ est un corps si, et seulement si, n est un nombre premier.

Cette propriété est démontrée dans le paragraphe Cas où Z/nZ est un corps de l'article Anneau Z/nZ.

Une question importante sera celle de la structure du groupe multiplicatif des corps finis. Ici :

• Si p est premier, alors le groupe des inversibles Z/p.Z^* est un groupe cyclique d'ordre p - 1.

Cette propriété est démontrée dans le paragraphe Cas où n est premier de l'article Anneau Z/nZ.

On verra plus loin que ces exemples sont en fait les seuls exemples de corps finis de cardinal un nombre premier, mais aussi que tout corps fini peut s'obtenir par extension algébrique à partir d'un tel corps. Si p est un nombre premier, F_p désigne le corps Z/p.Z.

Il existe des polynômes irréductibles P(X) de F_p [X] tel que le quotient F_p [X]/(P(X)) de l'anneau des polynômes F_p [X] par l'idéal principal engendré par un tel polynôme irréductible P(X) soit un corps fini (commutatif). Il contient strictement le corps premier d'ordre p, si le polynôme n'est pas de degré un. Ce corps n'est autre qu'un corps de rupture du polynôme : la classe de X fournit une racine de P. Ici X désigne une indéterminée et P(X) un polynôme formel. L'usage de polynômes formels à la place d'une fonction polynôme est indispensable, il existe des polynômes non-nuls dont les fonctions polynômes associées sont identiquement nulles sur F_p (par exemple X + X² sur F₂). Une autre manière de se rendre compte de la différence est qu'il ne peut exister qu'un nombre fini de fonctions de F_p dans F_p et donc de fonctions polynômes, alors qu'il existe un nombre infini de polynômes formels.

Par exemple, pour p=2, le polynôme 1+X+X² est irréductible dans F₂ [X] (c'est d'ailleurs l'unique polynôme irréductible de degré 2). L'extension correspondante est un corps noté F₄. Ce corps a exactement 4 éléments qui sont 0, 1, et les deux racines x et x+1 de 1+X+X². Ses lois sont données comme suit :

Le groupe multiplicatif des inversibles F_q^* est monogène, isomorphe au groupe cyclique Z/(q-1)Z. Dans notre exemple, F₄ est engendré par les puissances de la classe de x: x²=x+1, x³=1. La table de multiplication est facile à écrire en termes de ce groupe cyclique, mais c'est alors l'addition qui est moins commode.

Pour p > 2, la fonction polynomiale carrée, qui à x associe son carré x² n'est pas injective car envoie les éléments distincts 1 et -1 sur 1. Comme son ensemble de départ est égal à son ensemble d'arrivée et est un ensemble fini, la fonction n'est pas non plus surjective. Ainsi, il existe au moins un élément a tel que le polynôme P(X) égal à X² - a ne soit pas scindé. L'extension associée à ce polynôme est de degré 2 et fournit un corps contenant n = p² éléments noté F_n. À isomorphisme près, ce corps est indépendant de a.