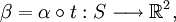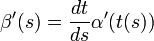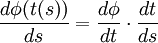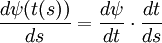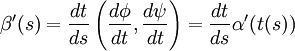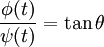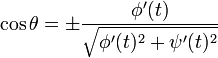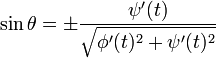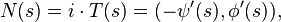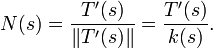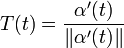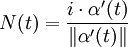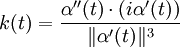Courbe plane - Définition
La liste des auteurs de cet article est disponible ici.
Reparamétrage
Soient
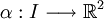
telle que pour tout
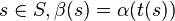
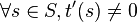
On vérifie alors le théorème suivant : si
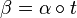
- Démonstration
- Si α(t) = (φ(t),ψ(t)) alors β(s) = (φ(t(s)),ψ(t(s))) et d'après les théorèmes de dérivation des fonctions composées, on a :
- et ainsi on obtient :
Cosinus directeurs
D'après la définition même de la dérivée, on obtient :
ce qui, d'un point de vue géométrique, représente la pente de la droite tangente à la courbe, autrement dit la tangente (au sens trigonométrique du terme) de l'angle que cette tangente forme avec l'axe horizontal (l'axe des 'x'). De cette relation, on peut extraire les cosinus directeurs de la tangente à la courbe :
Abscisse curviligne
On définit l'abscisse curviligne ou paramètre longueur d'arc comme étant le reparamétrage particulier obtenu en fixant la borne inférieure d'intégration a, de façon à ce que l'intégrale
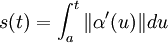
étant donné que  , on peut inverser s(t), et son inverse est t = t(s). Alors on obtient le reparamétrage par l'abscisse curviligne donné par : β(s) = α(t(s)).
, on peut inverser s(t), et son inverse est t = t(s). Alors on obtient le reparamétrage par l'abscisse curviligne donné par : β(s) = α(t(s)).
On démontre ensuite que le vecteur tangent est unitaire :
-
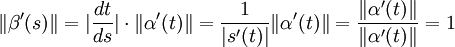
Longueur d'une courbe
Longueur d'un arc paramétré
Soient α(t) = (φ(t),ψ(t)) une courbe différentiable sur I, et
![[a,b]\subseteq I](https://static.techno-science.net/illustration/Definitions/autres/0/0c821dc116e0e2afe7e0856071a2479e_c8bdcb6b5aa0f01abde4fd9839edc669.png)
-
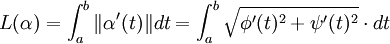
Si de plus β(s) est un reparamétrage de la courbe, alors :
-
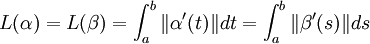
Longueur et forme cartésienne explicite
Si la courbe est représentée sous forme cartésienne explicite y = f(x) alors, comme
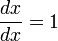
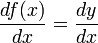
-
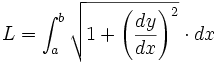
Paramétrage avec les coordonnées polaires planes
Une forme de paramétrage qui revêt une importance notable dans l'étude des mathématiques, de la géométrie et dans de nombreux domaines d'application des mathématiques, est celle des coordonnées polaires planes. Étant donnée une courbe paramétrée en coordonnées polaires par la forme cartésienne r = r(θ), avec c ≤ θ ≤ d, et par la forme paramétrée :
-
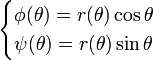
Alors ses dérivées sont :
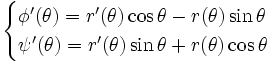
et donc la longueur de l'arc est :
-
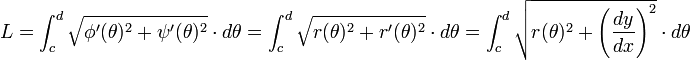
Formules de Frenet
Une courbe (suffisamment régulière) de l'espace possède, en tous ses points, un système de référence, dit trièdre de Frenet, donné par un triplet de vecteurs tangent, normal e binormal. Une telle courbe est plane si et seulement si le vecteur binormal est toujours nul.
Soit β(s) = (φ(s),ψ(s)) une courbe paramétrée selon l'abscisse curviligne. Le vecteur unitaire tangent est déterminé par :
- T(s) = β'(s) = (φ'(s),ψ'(s)).
Le vecteur unitaire normal est déterminé par :
où i est le nombre complexe tel que i2 = − 1. Grâce à la définition de la courbure, on peut donner une autre forme au vecteur unitaire normal :
On démontre que le vecteur T' est orthogonal à T et donc parallèle à N.
Finalement, les formules de Frenet et la courbure pour une courbe plane, quel que soit son paramétrage α(t) = (φ(t),ψ(t)), sont :