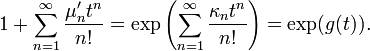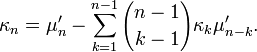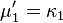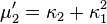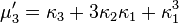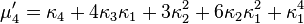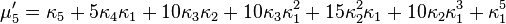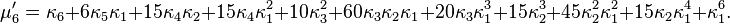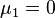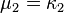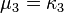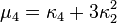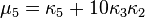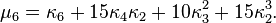Cumulants (statistiques) - Définition

Quelques propriétés des cumulants

Invariance

Les cumulants vérifient pour tout variable aléatoire X et tout constante c les relations: κ₁(X + c) = κ₁(X) + c et κ_n(X + c) = κ_n(X) pour n ≥ 2. Pour résumer, c est ajouté au premier cumulant, et tous les cumulants d'ordre supérieur sont inchangés.

Homogénéité

Le n-ième cumulant est homogène de degré n, c'est-à-dire si c est une constante, alors:

κ_n(cX) = cⁿκ_n(X).

Additivité

Si X et Y sont indépendants, alors κ_n(X + Y) = κ_n(X) + κ_n(Y).

Un résultat en demie-teinte

Sachant les résultats des cumulants de la loi normale, on pourrait espérer trouver des distributions pour lesquelles κ_m = κ_m+1 = ... = 0 pour un m>3, et où les cumulants d'ordre inférieur (ordres 3 à m -1) sont non-nuls. Il n'existe pas de telles distributions. Le résultat sous-jacent est que la fonction génératrice des cumulants ne peut être un polynôme de degré fini, et de degré plus grand que 2.

Cumulants et moments

La fonction génératrice des moments est :

si bien que la fonction génératrice des cumulants est le logarithme de la fonction génératrice des moments. Le premier cumulant est l'espérance; les deuxième et troisième cumulants sont respectivement les deuxième et troisième moments centrés (le moment centré d'ordre 2 est la variance); mais les cumulants d'ordre supérieur ne sont pas égaux aux moments non-centrés, pas plus qu'aux moments centrés. Ce sont plutôt des polynômes de ces moments.

Les cumulants sont liés aux moments par la formule de récurrence :

Le n-ème moment μ′_n est un polynôme de degré n des n premiers cumulants:

Les coefficients sont précisément ceux qui apparaissent dans la formule de Faà di Bruno.

Les moments μ′_n ne doivent pas être confondus avec les moments centrés μ_n. Pour exprimer les moments centraux en fonction des cumulants, il suffit d'ignorer tous les termes dans lesquels on trouve le facteur κ₁:

Cumulants de certaines lois continues

• Pour la loi normale, d'espérance μ et de variance σ², la dérivée de la fonction génératrice des cumulants est g '(t) = μ + σ²·t. Les cumulants sont donc κ₁ = μ, κ₂ = σ², et κ₃ = κ₄ = ... = 0. Le cas spécial σ² = 0 conduit à une variable constante: X = μ.

• Les cumulants pour la loi uniforme sur l'intervalle [−1, 0] sont κ_n = B_n/n, où B_n est le n-ième nombre de Bernoulli.

Histoire

Les cumulants ont été introduits en 1889 par l'astronome, mathématicien et actuaire danois Thorvald Nicolai Thiele (1838 - 1910) in 1889. Thiele les appelle alors half-invariants (demi-invariants). Il faut attendre 1931 pour trouver l'appellation cumulants dans le papier, The derivation of the pattern formulae of two-way partitions from those of simpler patterns, Proceedings of the London Mathematical Society, Series 2, v. 33, pp. 195-208, par le grand statisticien Ronald Aylmer Fisher et par John Wishart. L'historien Stephen Stigler reporte que le nom cumulant fut suggéré à Fisher dans une lettre de Harold Hotelling. La fonction de partition en physique statistique pour l'ensemble canonique a été introduit par Josiah Willard Gibbs en 1901.

Lien avec la physique statistique

En physique statistique, un système à l'équilibre avec un bain thermique à température T = 1 / β peut occuper des états d'énergie E. Soit f(E) la densité d'états d'énergie E. La fonction de partition du système est donné par

Z(β) = < exp( − βE) >

L'énergie libre du système est définie par

F(β) = ( − 1 / β)log(Z)

L'énergie libre du système donne accès à l'ensemble des propriétés thermodynamiques du système comme son énergie interne, son entropie, sa chaleur spécifique…