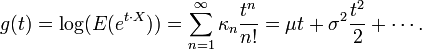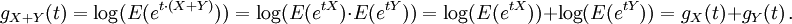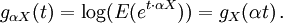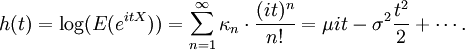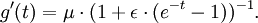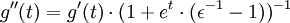Cumulants (statistiques) - Définition

Introduction

Dans la théorie des probabilités et en statistiques, une variable aléatoire X a une espérance mathématique μ = E(X) et une variance σ² = E((X − μ)²). Ce sont les deux premiers cumulants : μ = κ₁ et σ² = κ₂.

Les cumulants κ_n sont définis par la fonction génératrice des cumulants qui est g(t) :

Elle est donc intimement liée à la fonction génératrice des moments et à la fonction caractéristique de la variable X. Les cumulants sont donnés par les dérivées en 0 de g(t) :

κ₁ = μ = g' (0),

κ₂ = σ² = g' '(0),

κ_n = g⁽ⁿ⁾ (0).

Une distribution avec des cumulants κ_n donnés peut être approchée par un développement d'Edgeworth.

Comme indiqué plus haut, les cumulants d'une distribution sont liés aux moments de la distribution. Travailler avec la fonction génératrice des cumulants est plus pratique dans la mesure où pour des variables indépendantes X et Y,

tandis qu'avec la fonction génératrice des moments M_X, on obtient

.

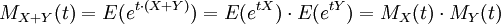
Il faut enfin remarquer que :

Certains auteurs préfèrent définir la fonction génératrice des cumulants directement à partir de la fonction caractéristique d'une variable aléatoire

La caractérisation des cumulants est valide même pour les distributions dont les plus hauts moments n'existent pas.

Cumulants de quelques distributions discrètes

• La variable aléatoire constante X = 1. La dérivée de la fonction génératrice des cumulants est g'(t) = 1. Le premier cumulant est donc κ₁ = g '(0) = 1 et tous les autres cumulants sont nuls, κ₂ = κ₃ = κ₄ = ... = 0.

• La variable aléatoire Y = μ se déduit de la variable aléatoire précédente. La fonction génératrice des cumulants est donc g_Y(t) = g_X(μt) = μt. Bref, chaque cumulant est juste μ fois les cumulants précédents. On a donc κ₁ = g '(0) = μ et les autres cumulants sont nuls, κ₂ = κ₃ = κ₄ = ... = 0.

• La loi de Bernoulli (nombre de succès dans une épreuve avec une probabilité de succès p). Le cas spécial p = 1 revient à la variable aléatoire X = 1. La fonction génératrice est g(t) = ln(pe^t + (1 − p)). Sa dérivée est g '(t) = ((p⁻¹−1)·e^−t + 1)⁻¹. Finalement, les cumulants sont κ₁ = g '(0) = p et κ₂ = g ' '(0) = p·(1−p) . Les cumulants vérifient la formule de récurrence

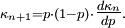
• La loi géométrique (nombre de défaillances avant un succès, avec une probabilité de succès p à chaque expérience). La dérivée de la fonction génératrice des cumulants est g '(t) = ((1−p)⁻¹·e^−t−1)⁻¹. Les premiers cumulants sont κ₁ = g '(0) = p⁻¹−1, et κ₂ = g ' '(0) = κ₁·p⁻¹. En posant p = (μ+1)⁻¹, on obtient g '(t) = ((μ⁻¹+1)·e^−t−1)⁻¹ et κ₁ = μ.

• La loi de Poisson. La dérivée de la fonction génératrice des cumulants est g '(t) = μ·e^t. Tous les cumulants sont égaux au paramètre: κ₁ = κ₂ = κ₃ = ...=μ.

• La loi binomiale (n répétitions indépendantes de l'expérience de Bernouilli décrite plus haut). Chaque cumulant est juste n fois le cumulant associé de la loi de Bernouilli. La dérivée de la fonction génératrice des cumulants est g '(t) = n·((p⁻¹−1)·e^−t + 1)⁻¹. Les premiers cumulants sont κ₁ = g '(0) = n·p et κ₂ = g ' '(0) = κ₁·(1−p). En posant p = μ·n⁻¹ cela donne g '(t) = ((μ⁻¹−n⁻¹)·e^−t+n⁻¹)⁻¹ et κ₁ = μ. Le cas limite n⁻¹ = 0 est une loi de Poisson.

• La loi binomiale négative (nombre d'échecs avant n succès avec une probabilité de succès p à chaque expérience). Le cas spécial n = 1 est la loi géométrique. La dérivée de la fonction génératrice des cumulants est g '(t) = n·((1−p)⁻¹·e^−t−1)⁻¹. The first cumulants are κ₁ = g '(0) = n·(p⁻¹−1), et κ₂ = g ' '(0) = κ₁·p⁻¹. En posant p = (μ·n⁻¹+1)⁻¹, cela donne g '(t) = ((μ⁻¹+n⁻¹)·e^−t−n⁻¹)⁻¹ et κ₁ = μ. Comparer ces formules à celles de la loi binomial permet de justifier le nom de 'loi binomiale négative'. Le cas limite n⁻¹ = 0 est encore la loi Poisson.

En introduisant , les distributions précédentes donnent une formule unifiée pour la dérivée de la fonction génératrice des cumulants :

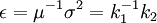
La dérivée seconde est

confirmant que le premier cumulant est κ₁ = g '(0) = μ et que le second cumulant est κ₂ = g ' '(0) = μ·ε. Les variables aléatoires constantes X = μ sont telles que є = 0. Les lois binomiales vérifient є = 1 − p si bien que 0<є<1. Les lois de Poisson vérifient є = 1 tandis que les lois binomiales négatives se caractérisent par є = p⁻¹ si bien que є > 1. Il faut noter l'analogie avec l'excentricité des coniques: cercles є = 0, ellipses 0 < є < 1, paraboles є = 1, hyperboles є > 1.