Déduction naturelle - Définition
La liste des auteurs de cet article est disponible ici.
Les règles fondamentales de la déduction naturelle
Les propositions au-dessus de la barre s'appellent les prémisses et la proposition sous la barre s'appelle la conclusion. La règle ci-dessus élimine le connecteur →. En fait, dans la déduction naturelle, il y a deux types de règles: des règles d'introduction et des règles d'élimination. Nous allons, dans un premier temps, présenter les règles qui régissent les connecteurs →, ∧ et ⊥.
- L'hypothèse
-
- Les règles d'introduction
-
![(\wedge I)\quad \frac{p\qquad q}{p\wedge q} \qquad \qquad (\to I)\quad \frac{\stackrel{\displaystyle[p]}{\stackrel{\vdots}{q}}}{p\to q}](https://static.techno-science.net/illustration/Definitions/autres/8/8c44fa4834ecf5b0d8e6e0c87849ca8a_393722f5548b497e8e600b4302877c4d.png)
- Dans la règle d'introduction de la flèche l'hypothèse p est déchargée, ce qui se dénote en la mettant entre crochets.
-
- Le règles d'élimination
-
- Les règles qui régissent ⊥ (faux)
- Ce sont deux règles qui éliminent ⊥, mais qui ont la particularité d'introduire une proposition. Comme souvent, on utilise la notation ¬p comme une abréviation de p → ⊥.
-
![(\perp)\quad \frac{\perp}{p} \qquad \qquad (RAA)\quad \frac{\stackrel{\displaystyle[\neg p]}{\stackrel{\vdots}{\perp}}}{p}](https://static.techno-science.net/illustration/Definitions/autres/5/5673b2d7d4cb33f7e4a17053eb3f727b_d5f3349054393ac1f4197bc782317fe1.png)
- La règle de de raisonnement par l'absurde (reductio ad absurdum) décharche également une hypothèse.
-
La signification des règles
Si l'on a une démonstration de p et une démonstration de q, on a une démonstration de p ∧ q, c'est ce que qu'énonce la règle (∧ I). La règle (→ I) dit que si de l'hypothèse p on peut déduire q alors on peut déduire p → q, l'hypothèse p est alors enlevée de l'ensemble des hypothèses, on dit qu'elle est déchargée. Les deux règles d'élimination du connecteur ∧ énonce que si l'on a une démonstration de p ∧ q on a immédiatement une démonstration de p (première règle) et on a aussi une démonstration de q (deuxième règle). La règle d'élimination de → est le modus ponens bien connu depuis Aristote. La règle (⊥) énonce le fait que de la proposition fausse on peut déduire n'importe quelle autre proposition. La règle (RAA) est celle du raisonnement par l'absurde, c'est elle qui donne à la déduction naturelle son caractère non intuitionniste (c'est-à-dire « classique »), dans ce cas l'hypothèse ¬ p est déchargée. On remarquera cependant que si la règle (⊥) peut être vue comme une règle d'élimination du connecteur ⊥, la règle (RAA) n'est pas une règle d'élimination, encore moins une règle d'introduction, on voit donc que cette règle créée un biais dans la régularité introduction-élimination de la déduction naturelle intuitionniste.
La page Calcul des propositions donne une variante de la déduction naturelle avec des séquents spécifiques, dit « naturels », où les hypothèses sont gardées comme un contexte et où les hypothèses n'ont pas à être déchargées, mais disparaissent du contexte.
Quelques exemples
- Soit à démontrer p ∧ q → q ∧ p.
-
-
![\frac {\displaystyle\frac {\displaystyle \frac{[p \wedge q]}{q}{\scriptstyle(\wedge E)} \qquad \frac{[p \wedge q]}{p}{\scriptstyle(\wedge E)} } {q\wedge p} {\scriptstyle(\wedge I)} } {p\wedge q\rightarrow q\wedge p} {\scriptstyle(\rightarrow I)}](https://static.techno-science.net/illustration/Definitions/autres/8/885922a8fa342115c0fb0e285e1bf681_239f11cc5c86580f5c861c96a92c2d01.png)
- Les deux hypothèses sont déchargées par la règle
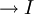
-
- Démontrons ¬¬p → p autrement dit ((p → ⊥) → ⊥) → p.
-
-
![\frac {\displaystyle\frac {\displaystyle\frac {[(p\rightarrow\bot)\rightarrow\bot]\qquad [p\rightarrow\bot]} {\bot} {\scriptstyle(\rightarrow E)} } {p} {\scriptstyle(RAA)} } {((p\rightarrow\bot)\rightarrow\bot)\rightarrow p} {\scriptstyle(\rightarrow I)}](https://static.techno-science.net/illustration/Definitions/autres/5/59bd48f1cc1f036062ca1d59155f172e_aa7579105e7c630b11e3a00251bfccc8.png)
- Ici les deux hypothèses sont déchargées chacune par une règle différente : l'hypothèse
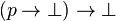

-
Les autres connecteurs et les quantificateurs
- Les règles de la disjonction
- Introduction
-
- Élimination
-
-
![\frac{p\vee q\quad\begin{array}[b]{c}[p]\\\vdots\\r\end{array}\quad\begin{array}[b]{c}[q]\\\vdots\\r\end{array}} {r}{\scriptstyle(\vee E)}](https://static.techno-science.net/illustration/Definitions/autres/0/068369ba0a14396e6d443453be062383_d7b76dbe4e59766766c8410af98db07f.png)
- Cette règle décharge les deux hypothèse p et q.
-
-
- Introduction
- Les règles de la quantification universelle
- En ce qui concerne la syntaxe, nous renvoyons à l'article calcul des prédicats. Nous ne donnons que les règles.
-
- Introduction
-
-
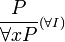
- à condition que la variable x n'apparaisse dans aucune des hypothèses non déchargées.
-
-
- Élimination
-
- Introduction
- Les règles de la quantification existentielle
- Introduction
-
- Élimination
-
-
![\frac{\exists x P\quad\begin{array}[b]{c}[P]\\\vdots\\q\end{array}} {q}{\scriptstyle(\exists E)}](https://static.techno-science.net/illustration/Definitions/autres/3/31282e955bde893a701fc1cd154d3751_459c558f1cd81c95487447a7247ffb2b.png)
- Cette règle décharge l'hypothèse P
-
-
- Introduction
On notera l'analogie qui n'est pas fortuite entre les règles du connecteur


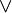
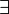
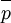


![\frac{\forall x P}{P[a/x]}{\scriptstyle(\forall E)}](https://static.techno-science.net/illustration/Definitions/autres/5/552aaa628efe47980384c96e62df52ad_0ae7ea62e91fe2b688162be39d932103.png)
![\frac{P[a/x]}{\exists x P}{\scriptstyle(\exists I)}](https://static.techno-science.net/illustration/Definitions/autres/b/b1a830cb4c252f87ce9736d700f602a6_977bf39d2d64ccb92b9e66f31e7d9f4c.png)

















































