Diagramme de Bondi - Définition

Introduction

Les diagrammes d'Hermann Bondi ont été conçus par leur inventeur afin de présenter graphiquement une méthode intuitive de compréhension de la Relativité restreinte. Ils sont destinés à des élèves en fin d'études secondaires.

Historique

En 1964, quand Hermann Bondi publie Relativity and Common Sense il est, entre autres, professeur de mathématiques appliquées au King's College de l'Université de Londres.

La méthode de calcul de Bondi, en relativité restreinte, est destinée à faciliter la compréhension des phénomènes de dilatation du temps, de compression des distances, de relativité de la simultanéité, sans passer par la transformation de Lorentz. Elle présente ces phénomènes d'une façon originale, à partir de l'effet Doppler.

C'est cet effet Doppler, dont l'application aux vitesses relatives relativistes permet d'établir un rapport entre la fréquence d'émission d'un signal et sa fréquence de réception, ce rapport étant de k, qui a donné son nom en anglais à la méthode d'Hermann Bondi : Bondi's k-calculus.

Cette méthode, destinée aux élèves de fin d'études secondaire, d'après le physicien Fred I. Cooperstock, fait l'objet dans son livre General Relativistic Dynamics d'un long développement basé sur le livre de Bondi, Lectures on General Relativity, paru en 1965.

C'est également avec cette méthode, et sa représentation graphique, que Fred I. Cooperstock présente dans ce document une résolution, qu'il qualifie de simple, du paradoxe des jumeaux, au chapitre 3.5, page 40 : The twin or clock paradox.

Résolution du paradoxe des jumeaux et des horloges par la méthode de Bondi

Figure 4 - Sur ce schéma, quand B rencontre C (en P), qui va vers A à la vitesse opposée , il cesse d'émettre vers A. Si B émet pendant T, A reçoit durant kT, car B s'éloigne. L'émission de C, pendant T aussi, est reçue par A pendant T/k, par C s'approche. Quand B fait un aller-retour de durée 2T (vu par B), ce voyage dure T(k + 1/k) vu par A.

B (Bernard) part en voyage à une vitesse relativiste et revient vers A (Alain), son jumeau. D'après la théorie de la relativité restreinte, la façon dont s'écoule le temps pour le voyageur Bernard fait qu'il reviendra moins âgé que Alain, qui est resté fixe. Selon la vitesse et la durée du voyage, Bernard retrouvera son frère jumeau Alain, devenu plus vieux que lui, ou même ne retrouvera que ses enfants, ou des descendants plus lointains. Si l'on inverse le point de vue, considérant alors que c'est Alain qui voyage, et Bernard qui représente le référentiel au repos, ne devrait-on pas trouver que c'est Alain qui est plus jeune que Bernard lors de leurs retrouvailles, ce qui serait paradoxal, car chacun des deux jumeaux ne peut être à la fois plus jeune et plus vieux ? (Voir l'article Paradoxe des jumeaux)

La résolution par la méthode de Bondi est représentée sur la figure 4 : B et A initialisent leurs horloges au moment du départ (au point O). Dès le départ, B émet des signaux en direction de A. Au bout d'un temps T (pour B), B croise un mobile C (au point P), arrête d'émettre vers A, alors que C prend le relai et émet à son tour vers A. Le mobile C est animé par rapport à A, d'une vitesse opposée à celle de B (v pour B, - v pour C).

B émet des signaux pendant une durée T. Comme B s'éloigne, A les reçoit pendant kT. C émet aussi pendant T, mais comme il s'approche de A à une vitesse - v, A les reçoit durant T/k. Pour A l'arrivée de C s'est effectuée après une durée de T( k + 1/k).

Considérant que le problème est équivalent à « Bernard fait demi-tour quand il s'est déplacé pendant un temps T », son voyage, pour lui, a duré 2T, alors que Alain, au repos, a compté kT + T/k sur son horloge.

En prenant un exemple numérique, si v = 0,8c (80% de la vitesse de la lumière), le facteur Doppler .

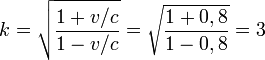
Si Bernard met T = 1 an dans son référentiel avant de faire demi-tour, il fera son voyage en deux ans alors qu'Alain aura vieilli de (1x3 + 1/3 = 3,33) ans, soit trois ans et quatre mois dans son référentiel au repos.

Cela parait évident pour Hermann Bondi et Fred Cooperstock que la démonstration se suffit à elle-même sans qu'il soit besoin de mettre Bernard dans un référentiel au repos et Alain dans un référentiel mobile : aucun diagramme, où les situations seraient inversées, n'est présenté.

Les seules considérations, d'après eux, pouvant amener à controverse sont celles qui concernent le fait, qu'en réalité, si l'on pouvait reproduire physiquement l'expérience de pensée, seul Bernard serait soumis à des accélérations, au départ, au demi-tour, à l'arrivée, et que ces périodes accélérées ne pourraient pas compenser la différence de durée entre les référentiels, car elles sont indépendantes de la durée du voyage. Ces phases d'accélération ne sont donc pas des arguments recevables pour une éventuelle remise en cause de la démonstration, prouvant que le voyage a duré moins longtemps pour Bernard que pour Alain.