Dimension d'un espace vectoriel - Définition

Introduction

En algèbre linéaire, la dimension de Hamel ou simplement la dimension est un invariant associé à tout espace vectoriel E sur un corps K. La dimension de E est le cardinal commun à toutes ses bases. Ce nombre est noté dim_K(E) (lire « dimension de E sur K ») ou (s'il n'y a aucune confusion sur le corps des scalaires K) ou encore [E:K]. Si E admet une partie génératrice finie, alors sa dimension est finie et elle vaut le nombre de vecteurs constituant une base de E.

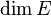
Cette définition repose d'une part sur l'existence de bases, corollaire du théorème de la base incomplète, et d'autre part sur le théorème de la dimension pour les espaces vectoriels, qui assure que deux bases d'un même espace ont même cardinal. Cette dimension porte parfois le nom du mathématicien allemand Georg Hamel. A isomorphisme près, les K-espaces vectoriels sont classifiés par leurs dimensions. Une terminologie est spécifique aux espaces de petite dimension :

• Espace nul : désigne un espace E de dimension nulle. Il admet comme unique élément son vecteur nul. La famille vide est une famille libre maximale, c'est l'unique base de E, et ne comporte aucun vecteur.
• Droite vectorielle ou droite : désigne un espace vectoriel E de dimension 1. Tout vecteur non nul de E forme une base de E.
• Plan vectoriel ou plan : désigne un espace vectoriel E de dimension 2. Toute paire (u,v) de vecteurs non colinéaires de E forme une base de E.

Exemples

La dimension d'un espace vectoriel peut être calculée en choississant une base canonique :

• Le corps K, vu comme espace vectoriel, est de dimension 1. Pour tout entier naturel n>0, le produit cartésien Kⁿ est l'espace vectoriel des n-uplets de scalaire. Il est de dimension n, sa base canonique comportant exactement n vecteurs. Il suit de la définition que toute base de Kⁿ comporte exactement n vecteurs.
• Plus généralement, pour tout ensemble A, on note K^(A) l'ensemble des familles des éléments de K indexée par A et à support fini. L'addition et la multiplication par un scalaire étant définis terme à terme, K^(A) est un espace vectoriel sur K. Sa base canonique est la famille , où pour . Il s'en suit que la dimension de K^(A) est le cardinal de A.
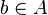
• Les polynômes à coefficients dans un corps de degré inférieur ou égal à n forment un sous-espace vectoriel E de K[X], dont la dimension est n + 1. La famille est une base canonique de E.
• L'espace vectoriel des matrices à n lignes et p colonnes à coefficients dans un corps , est de dimension . La famille (E_ij) constituée des matrices ayant un 1 à la ième ligne et jème colonne et des zéros partout ailleurs est une base de cet espace vectoriel.

Le choix du corps des scalaires a son importance.

• L'ensemble des nombres complexes peut être considéré à la fois comme un -espace vectoriel et comme un -espace vectoriel; nous avons et .

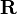
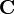
Généralisation

Il est possible de voir un espace vectoriel comme un cas particulier d'un matroïde, et pour ce dernier il y a une notion bien définie de dimension. La longueur d'un module et le rang d'un groupe abélien ont tous deux plusieurs proprétés similaires à la dimension des espaces vectoriels.

Propriétés

Si F est un sous-espace vectoriel de E, alors .

Pour démontrer que deux espaces vectoriels de dimension finie sont égaux, on utilise souvent le théorème suivant: Si E est un espace vectoriel de dimension finie et F un sous-espace vectoriel de E tels que dimF = dimE, alors E = F. Cette implication devient fausse en dimension infinie. Un important résultat sur la dimension concernant les applications linéaires est le théorème du rang.

Classification

Deux espaces vectoriels sur sont isomorphes en dimension finie si et seulement s'ils ont même dimension.

Toute application bijective entre leurs bases peut être prolongée de manière unique en un isomorphisme entre les deux espaces vectoriels. Si A est un ensemble, un espace vectoriel de dimension | A | sur peut être construit de la manière suivante: on considère l'ensemble de toutes les fonctions telles que f(a) = 0 pour un nombre fini d'éléments a de A. Ces fonctions peuvent être additionnées et multipliées par un scalaire de , et nous obtenons le -espace vectoriel recherché.

Modification de K

Soit L / K est une extension de corps. Alors L est un espace vectoriel sur K, la somme vectorielle étant la somme dans le corps L, et la multiplication par un scalaire étant la restriction à de la multiplication dans L. La dimension de L sur K s'appelle l'indice de l'extension. La définition est reprise et commentée dans l'article extension de corps.

De plus, tout L-espace vectoriel E est aussi un K-espace vectoriel, par restriction de la multiplication. Les dimensions sont liées par la formule:

.

En particulier, tout espace vectoriel complexe de dimension n est un espace vectoriel réel de dimension 2n.

Dimension et cardinal

La dimension de l'espace vectoriel K^(A) est le cardinal de A. De cette affirmation découle la relation suivante, qui relie le cardinal du corps des scalaires K, le cardinal de l'espace vectoriel E, et sa dimension sur K.

• Si dim_KE est finie, alors | E | = | K | ^dimE.
• Si dim_KE est infinie, alors | E | = max(dimE, | K | ).

En particulier, un K-espace vectoriel E est fini ssi K est fini et E est de dimension finie.

En particulier, un corps fini L peuit être vu comme un espace vectoriel sur son corps premier K, qui est de cardinal un nombre premier p, appelé la caractéristique de L. Si n est la dimension de L sur K, alors L est de cardinal pⁿ. Le cardinal de tout corps fini est une puissance entière de sa caractéristique.