Dynamique de rotation - Définition

Introduction

Dans un système matériel, d'après la loi des actions mutuelles (autrefois action et réaction) de Newton (cf lois du mouvement de Newton, énoncées en 1687), le torseur des forces intérieures au système est nul. Le principe fondamental de la dynamique s'écrit donc :

      Torseur dynamique = Torseur des forces extérieures      

Ces 6 équations se divisent en 2 groupes de 3 équations :

le principe fondamental de la dynamique de translation :

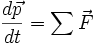
le principe fondamental de la dynamique de rotation :

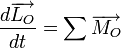
(somme des moments des forces extérieures pris par rapport au point O).

Ici, ΣF est somme des forces extérieures, p est la quantité de mouvement, O est un point fixe du référentiel galiléen. L_O est le moment cinétique du système pris par rapport à O. Sa dérivée temporelle s'appelle le moment dynamique M_O, somme des moments des forces extérieures réduites au point O.

Si le référentiel n'est pas galiléen, il convient simplement de rajouter le torseur des forces d'inertie d'entraînement et le torseur des forces d'inertie de Coriolis.

Cas de la rotation d'un solide autour d'un axe fixe

Soit ( O, k ) cet axe fixe. Soit θ, l'angle de rotation du solide prise par rapport à une direction fixe (disons (O,i)).

L'analyse des forces est : forces extérieures appliquées au solide + forces de réaction d'axe (inconnues a priori, mais bloquant la position du point O qui reste immobile, et dont la projection du moment sur l'axe est nulle) :

Alors l'équation du principe fondamental de la rotation projetée sur l'axe donne : .

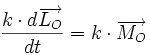
formulation bac +1

Or L(O) = I(O) k . ω , avec ω = dθ/dt, et I(O) l'opérateur linéaire d'inertie ( ne pas s'affoler, on n'en aura pas besoin!)

La quantité scalaire k.I(O)k s'appelle inertie à la rotation ( anciennement moment d'inertie de rotation), souvent nommée J (en ex-math_elem; ou C dans les cours de S.I.(sciences industrielles)).

Le PFDR (le principe fondamental de la dynamique de rotation) s'écrit alors :

      J dω/dt = Mz      

ce qui est l'exacte transposition à la rotation du PFDT ( principe fondamental de la dynamique de translation sur un axe):

      m d v/ dt = F      

De ce fait , tout ce qui a été dit sur le problème précédent est traduisible; simplement l'inertie à la rotation J vient remplacer l'inertie à la translation m.

formulation Bac

Soit à calculer k.L(O): le solide est formé de millions de points matériels M_i, de masse m_i, de projection sur l'axe H_i, décrivant lors de la rotation du solide des cercles de centre H_i, de rayon d_i = H_iM_i : chaque masse a donc un moment cinétique projeté sur l'axe égal à :

 :

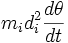
on appelle inertie à la rotation J la somme .

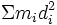
Le PFDR s'écrit alors :

      J dω/dt = Mz ,      

      l'inertie à la rotation est en kg.m^2;et Mz en N.m      

ce qui est l'exacte transposition à la rotation du PFDT ( principe fondamental de la dynamique de translation sur un axe):

      m d v/ dt = F      

De ce fait , tout ce qui a été dit sur le problème précédent est « translatable »; simplement l'inertie à la rotation J vient remplacer l'inertie à la translation m.

Quelques cas classiques

Le cylindre de révolution creux : toute la masse est à la distance R de l'axe : J = M.R^2

Le barreau de révolution plein, de densité uniforme de rayon R : J =1/2 . M.R^2

La sphère creuse de rayon R : 2/3 M.R^2

La boule pleine de densité uniforme : 2/5 M.R^2

Ces calculs sont aisément faits ( cf calculs d'inertie à la rotation )

Le théorème de Huygens

Historiquement, c'est un tour-de-force ! car Huygens n'avait à sa disposition que la loi de Torricelli ( cf Histoire des sciences :pendule pesant ): Soit J° l'inertie de rotation du solide par rapport à son centre d'inertie G : l'inertie de rotation J par rapport à un axe parallèle, distant de d, vaut J = J° + M.d^2

Il est alors facile de calculer l'inertie de rotation J° d'un barreau de longueur 2a : J° = M a^2 /3, de longueur 2a et de largeur 2b : J° = M (a^2+b^2)/3.

Application classique: le pendule pesant

voir pendule pesant