Émile Lemoine - Définition

Rôle dans la géométrie moderne du triangle

Lemoine est décrit par Nathan Court comme le co-fondateur (avec Henri Brocard et Joseph Neuberg) de la géométrie moderne du triangle, un terme utilisé par William Gallatly entre autres. Une telle géométrie repose sur l'abstraction des figures du plan plutôt que sur les méthodes analytiques utilisées auparavant et impliquant des mesures d'angles et de distances spécifiques. Cette géométrie est axée sur des sujets tels que la colinéarité, la concourance et la cocyclité, car ceux-ci n'impliquent pas les mesures énumérées précédemment.

Les travaux de Lemoine ont défini beaucoup des caractéristiques célèbres de ce mouvement. Sa Géométrographie, les relations entre des équations et des tétraèdres et triangles, et son étude de la concourance et de la cocyclité ont contribué à l'époque à la géométrie moderne du triangle. La définition des points du triangle comme le « point de Lemoine » est un élément de base de la géométrie, et d'autres géomètres modernes du triangle tels que Brocard et Gaston Tarry ont écrit des papiers sur des points similaires.

Travaux

Ses principaux travaux de recherche concernent la géométrie, en particulier la géométrie projective, la géométrie descriptive et la statique graphique. Sous le terme de « géométrie moderne du triangle », il développe particulièrement la théorie des transversales et des polaires, obtenant quelques résultats célèbres parmi lesquels le « point de Lemoine » et le « cercle de Lemoine ».

En 1902, à l'Université de Paris, Lemoine reçoit le prix Francœur d'une valeur de 1 000 francs, prix qu'il a détenu pendant plusieurs années : de 1902 jusqu'à sa mort en 1912, sauf en 1905.

La postérité de son œuvre est néanmoins moins grande que ce que laissaient imaginer les débuts prometteurs de la géométrographie ; les calculateurs graphiques n'ayant pas adopté les constructions de Lemoine, certes optimisées mais difficiles à retenir.

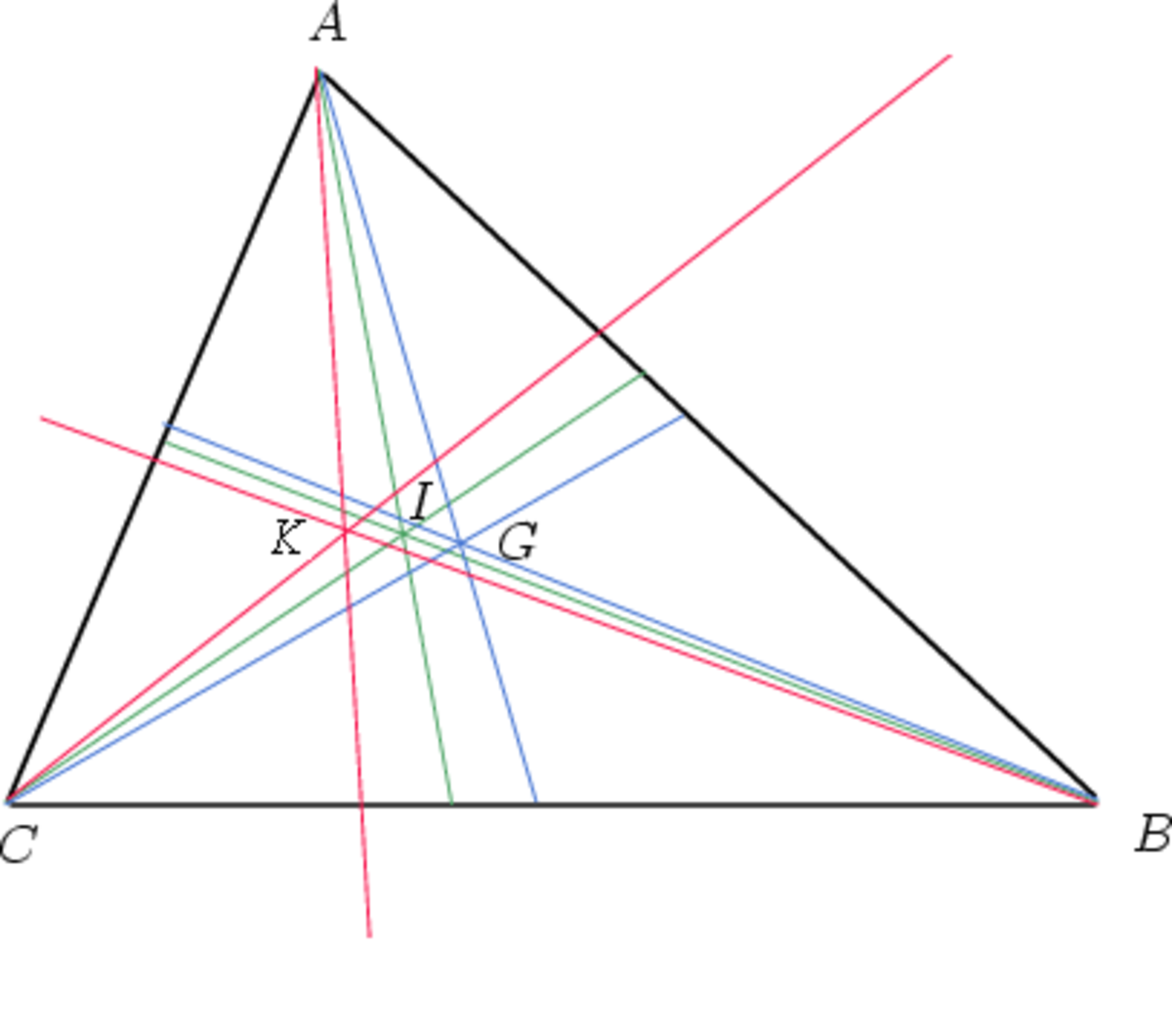
Point et cercle de Lemoine

Ici, K est le point symédian, dit « point de Lemoine ». En bleu les médianes, en vert les bissectrices, en rouge les symédianes (symétriques des médianes par rapport aux bissectrices).

Dans sa publication de 1874 nommée Note sur les propriétés du centre des médianes antiparallèles dans un triangle, Lemoine prouve que les symédianes d'un triangle (symétriques des médianes par rapport aux bissectrices) sont concourantes. Cet article contient d'autres résultats comme celui qui énonce qu'une symédiane partant d'un sommet coupe le côté opposé en segments dont le ratio est égal au ratio des carrés des deux autres côtés.

Lemoine a aussi démontré que si on trace des droites parallèles aux côtés du triangle et passant par le point symédian, alors les six points d'intersection entre ces droites et les côtés du triangle sont cocycliques, c'est-à-dire qu'ils se situent sur un même cercle. Ce cercle est maintenant connu sous le nom de « premier cercle de Lemoine », ou plus simplement « cercle de Lemoine ».

Classification des constructions géométriques

La classification des constructions géométriques de Lemoine, la Géométrographie, tente de créer un système méthodologique par lequel les constructions peuvent être jugées. Le système permet un procédé plus direct pour simplifier les constructions existantes. Dans sa description, il a listé cinq opérations principales : placer la pointe du compas sur un point donné, le placer sur une droite donnée, tracer un cercle avec le compas placé sur un point ou une droite donnée, placer la règle sur une droite donnée et prolonger la droite avec la règle.

La « simplicité » d'une construction peut être mesurée par le nombre des opérations qu'elle exige. Dans son article, Lemoine examine l'exemple du problème des contacts, initialement posé par Apollonius de Perge durant l'époque hellénistique et concernant la méthode de construction d'un cercle tangent à trois cercles donnés. Le problème, ressuscité au XVIe siècle par François Viète, avait été résolu par Joseph Diaz Gergonne en 1816 avec une construction de simplicité 400, mais la solution présentée par Lemoine a une simplicité de 199. Des solutions plus simples, comme celle de Frederick Soddy en 1936 et de David Eppstein en 2001, sont maintenant connues.

Conjecture de Lemoine

Lemoine publie en 1894 une conjecture en théorie des nombres, concernant les nombres premiers, qui porte désormais son nom ; même si elle est souvent surnommée conjecture de Levy dans les pays anglo-saxons, suite à un article de Hyman Levy. Cette conjecture, similaire à (mais plus forte que) la conjecture de Goldbach, énonce que

, où désigne les nombres premiers,

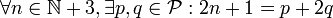
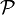
c'est-à-dire tout nombre impair supérieur à 5 est la somme d'un nombre premier et du double d'un autre nombre premier.