Énergie pneumatique - Définition
La liste des auteurs de cet article est disponible ici.
Principes de mise en œuvre
Un système pneumatique repose sur une différence de pression entre deux zones, différence de pression qui crée une force mécanique.
La force (F) résultant de la différence de pression entre les deux zones est proportionnelle à la différence de pression (P1 - P2) et à la surface (S) sur laquelle elle s'exerce : F = (P1 - P2) * S
Toute la matière fermant la zone subira cette force, tant qu'elle peut y résister.
Si la zone est fermée par une partie déformable et/ou mobile, que l'on nomme « piston », alors le piston bougera, en modifiant le volume des zones.
Selon la conception du système, le piston bougera par exemple de manière linéaire, à l'intérieur d'un cylindre.
Il peut bouger avec un mouvement de rotation, plus ou moins complexe, on peut parler alors de « turbine ».
Dans les armes servant à lancer des projectiles, le projectile est le piston, animé d'une très grande vitesse linéaire, combinée à une rotation servant à le stabiliser sur sa trajectoire.
Un avion est porté par ses ailes, qui forment un piston entre la zone avec moins de pression, au-dessus de l'aile, par rapport à la zone sous l'aile.
Enfin, le piston peut être déformable (ballon, diaphragme) voire être liquide (baromètre à mercure, bulle) et des phénomènes de dissolution et de vaporisation entrent en jeu.
Souvent, l'une des zones est à la pression atmosphérique. Il s'agit d'une référence pratique, mais la pression atmosphérique varie selon le lieu, selon son altitude et selon les conditions météorologiques.
Classification par fonction
Les systèmes pneumatiques utilisent quatre fonctions principales :
Des composants supplémentaires vont être utilisés dans les systèmes :
- vanne ;
- échangeur thermique ;
- détendeur ou régulateur de pression ;
- régulateur de débit ;
- clapet anti-retour ;
- filtres ;
- capteurs pour les mesures de paramètres.
Si la modularité (1 matériel = 1 fonction) est toujours recherchée pour la simplification de la conception et la standardisation de la production, certains matériels peuvent combiner plusieurs fonctions pour des raisons d'optimisation.
Estimation de l'énergie
Estimation à valider (provenance article véhicule à air comprimé)
Un réservoir de volume V contenant de l'air à la pression Pa qu'on laisse se détendre contient effectivement de l'énergie mécanique qu'on peut récupérer.
Dans le meilleur des cas (détente adiabatique réversible, rendement égal à 100 %), la puissance délivrée (en J/kg d'air) sera :
![W= -\frac{\gamma}{\gamma-1}* Z * r * Ta * [{\frac{Pr}{Pa}}^{(\frac{\gamma-1}{\gamma})} - 1]](https://static.techno-science.net/illustration/Definitions/autres/b/b064f7603ff4fa4856eae6562fa7c84b_ae811d44401a1541676929abd4001735.png)
avec gamma = Cp/Cv = 1,4 pour de l'air Z = coefficient de compressibilité = 1 r = constante du gaz = R/M R= 8,314 J/mole.K et M masse molaire en kg/mole (= 0,028 pour de l'air) Ta = température absolue (en °K) à l'aspiration = t (en °C) +273
Si t = 27 °C alors Ta = 300 °K Si Pr =1 bar ( = atmosphère) alors W = -311 775*[(1/Pa)^0,286 -1)
pour Pa = 300 bar W = 250,76 kJ/kg et Ro = 423 kg/m³ pour Pa = 100 bar W = 228,24 kJ/kg et Ro = 141 kg/m³
où Ro est la masse volumique de l'air à la pression considérée
Si on a un réservoir de 300 litres (soit cinq fois un réservoir normal), soit 0,3 m³ pour Pa = 300 bar on a 126 kg d'air (en supposant le gaz parfait, ce qui n'est vraiment exact dans cette gamme de pression) pour Pa = 100 bar on a 42 kg d'air
On peut donc produire (en supposant que la pression est toujours maximale jusqu'à l'utilisation du dernier kg d'air ce qui majore considérablement ...) pour Pa = 300 bar Energie = 31 500 kJ = 8,75 kWh pour Pa = 100 bar Energie = 9 576 kJ = 2,7 kWh
Estimation à valider (provenance article air comprimé)
L'énergie
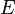
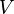
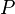
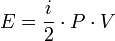
i = 3 pour un gaz monoatomique, ( par exemple du He )
i = 5 pour un gaz diatomique et ( par exemple de l'O2 ou du N2 )
i = 6 pour un gaz triatomique ou plus ( par exemple du CO2 )
Cette énergie peut être récupérée par décompression adiabatique, c'est-à-dire sans échange de chaleur avec l'environnement.
Si l'on fait une décompression isotherme, c'est-à-dire à température constante, on peut récupérer plus d'énergie, car une partie vient de l'environnement sous forme de chaleur.
Dans ce cas, l'énergie récupérée vaut :
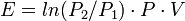
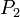
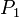
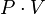
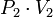
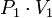
Par exemple :
l'énergie contenue dans 300 litres d'air ( 0,3 m3 ) à 300 bars
![\scriptstyle(\; 3 \cdot 10^7 [N/m^2]\; )](https://static.techno-science.net/illustration/Definitions/autres/a/accdb6b5f78aeeff371ef9e50dc51816_47c967f5af72513aa2817cccd7e7e6ea.png)
![\scriptstyle E \;=\; \frac{6}{2} \cdot 3 \cdot 10^7 \cdot 0,3 \;=\; 27 \;[MJ]](https://static.techno-science.net/illustration/Definitions/autres/2/292af0ec96ba9cfd3868b2797c99b8f0_075220b97d6598d5edc25e9c0d56e314.png)
Ceci correspond à l'énergie contenue dans 0,6 [kg] d'essence, soit 0,83 litres d'essence.
Si la décompression est isotherme,
![\scriptstyle {E \;=\; ln(300/1) \cdot 3 \cdot 10^7 \cdot 0,3 \;=\; 51,3 \;[MJ]}](https://static.techno-science.net/illustration/Definitions/autres/e/e24e112d17fab96c05fa0b77e6cddf79_68a7970431d19f48bd91beec2eb1e264.png)
Ceci correspond à l'énergie contenue dans 1,14 kg d'essence, soit 1,6 litre d'essence.