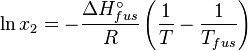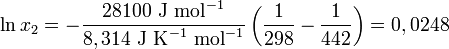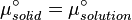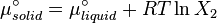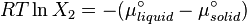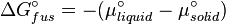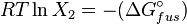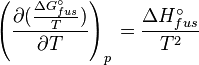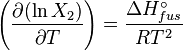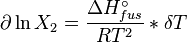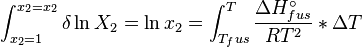Enthalpie de fusion - Définition

Détermination de la solubilité

La chaleur de fusion peut être aussi utilisée pour déterminer la solubilité des solides dans les liquides.

Dans une solution parfaite, la fraction molaire (x₂) du soluté à saturation est une fonction de la chaleur de fusion, du point de fusion du solide (T_fus) et de la température (T) de la solution :

Avec, R étant la constante universelle des gaz parfaits. Par exemple, la solubilité du paracétamol dans l'eau à 298 K est déterminée par :

Ce qui est égal à la solubilité en gramme/litre de :

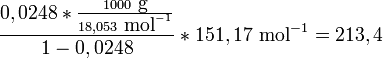
qui dévie de la solubilité réelle (240 g/l) de 11%. Cette erreur peut être réduite en incluant dans la formule, un paramètre de capacité thermique massique.

Preuve

À léquilibre, les potentiels chimiques d'un solvent pur et d'un solide pur sont identiques :

ou

avec la constante universelle des gaz parfaits et la température.

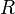
Le réarrangement donne :

d'où l'on tire :

la chaleur de fusion étant la différence de potentiel chimique entre le liquide pur et le solide pur, il s'ensuit :

Application de la relation de Gibbs-Helmholtz :

ce qui donne finalement :

ou :

et avec l'intégration :

le résultat final est obtenu par :

Applications

Pour chauffer un kilogramme (env. 1 litre) d'eau de 283,15 K à 303,15 K (10°C à 30°C), il faut 83,6 kJ.

Cependant, fondre de la glace puis augmenter la température de l'eau résultante de 20 K demande de l'énergie supplémentaire. Pour fondre de la glace à 273,15 K, puis chauffer l'eau résultante jusqu'à 293.15 K demande :

(1) 333,55 j/g (chaleur de fusion de la glace) = 333,55 kJ/kg = 333,55 kJ pour 1 kg de glace à fondre

PLUS

(2) 4,18 j/(g·K) = 4,18 kJ/(kg K) = 83,6 kJ pour 1 kg d'eau amenée à 20 K

au total = 417,15 kJ