Entier de Dirichlet - Définition

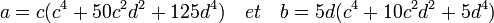
1. il existe quatre entiers relatifs m, n, t, u tel que a + b.√5 = 1/2.(t + u.√5).[1/2.(m + n.√5)] ⁵ où 1/2.(t + u.√5) est une unité et 1/2.(m + n.√5) est un entier de Dirichlet (donc m et n ont même parité).

a² - 5.b² est le produit de a + b.√5 et de son conjugué. Si a + b.√5 est premier avec son conjugué, alors il est le produit d'une puissance cinquième et d'une unité car l'anneau de Dirichlet est euclidien donc factoriel.

Soit d un entier de Dirichlet premier ou une unité, divisant a + b.√5 et son conjugué, il existe alors e et f deux entiers de Dirichlet tel que:

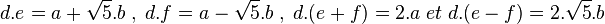
Si d divise √5, comme √5 est premier dans les entiers de Dirichlet, d est égal à √5 à une unité près. Comme 2 est aussi premier dans les entiers de Dirichlet, √5 divise a et 5 divise a² et donc a.0r 5 divise b, de plus a et b sont premiers entre eux. Donc 5 ne peut diviser a et par voie de conséquence √5 ne divise pas d.

2 ne peux pas diviser d car alors deux divise a + b.√5 et a/2 + √5.b/2 serait élément des entiers de Dirichlet, ce qui est incompatible avec le fait que a et b sont de parités différentes. En conséquence, d divise a et b. Le conjugué de d divise aussi a et b car ils sont entiers relatifs, et le produit de d et de son conjugué divise aussi a et b car d et son conjugué sont premiers entre eux (d est soit premier soit une unité). Ce produit est un entier, il est donc égal à ±1. En conclusion, les seuls entiers de Dirichlet qui divisent a + b.√5 et son conjugué sont des unités, la première remarque permet alors de conclure et :

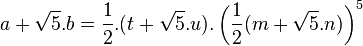
2. Il est possible de choisir m et n tel que t soit égal à 1 et u à 0.

Notons 1/2.(α + √5.β) = [1/2.(m + √5.n)]⁵. Montrons que β est un multiple de cinq et que α ne l'est pas. L'égalité s'écrit en développant l'égalité avec la formule du binôme :

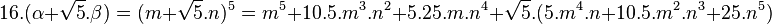
β apparaît clairement comme un multiple de cinq, si α l'est, alors a + b.√5 l'est aussi et comme b l'est, a l'est aussi. Or a n'est pas un multiple de cinq car b l'est et a et b sont premiers entre eux (dans l'ensemble des entiers relatifs).

Montrons alors que u est aussi un multiple de cinq :

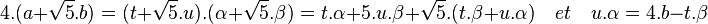
Cinq est multiple de b et de β, donc α.u est multiple de cinq. comme α n'est pas multiple de cinq, u l'est.

Montrons que t + u.√5 est une puissance cinquième. Tout élément du groupe de l'unité est une puissance positive soit de ω, soit de -ω, soit de soit de - et donc :

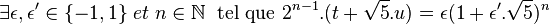
Une nouvelle utilisation de la formule du binôme montre l'égalité suivante et le fait que n est un multiple de cinq:

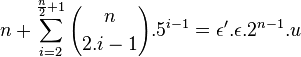
Comme n est une puissance de cinq il existe une unité θ tel que t + √5.u = θ⁵. En conclusion [θ.(m + √5.n)]⁵ est égal à a + √5.b. Ce qui revient à dire que l'unité peut être choisie égale à 1.

3. m et n sont pairs.

La formule du binôme montre, en développant l'égalité a + √5.b = (m + √5.n)⁵ :

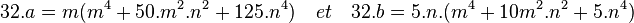
Supposons que m et n soient impairs, alors m⁴ + 10.m².n² + 5.n⁴ est congru à 0 modulo 32 car ni 5 ni n ne sont pairs. Les puissances quatrièmes de nombres impairs ne sont congrus qu'à 1 ou à 17 modulo 32. Il existe donc quatre cas à étudier. Considérons le premier cas : n et m ont une puissance de 4 congru à 1 modulo 32. Leurs carrés sont congrus soit à 1 soit à 17, et le produit de leurs carrés est alors congru soit à 1 soit à 17. L'expression est alors congru soit à 7 soit à 23. En conséquence, n et m ne peuvent posséder tout deux une puissance de 4 congru à 1 modulo 32 car l'expression doit être congru à 0. L'analyse des trois autres cas est analogue et tout aussi impossible. On en conclut que m et n sont nécessairement pairs.

4. Fin de la démonstration.

Alors l'égalité s'écrit a + b.√5 = (c + d.√5) ⁵ où 2.c = m et 2.d = n. En choisissant le signe de c (respectivement d)comme égal à celui de a (respectivement b) on obtient :

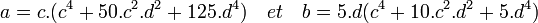
Si c ou d sont nuls, alors soit a soit b est nul, ce qui n'est pas le cas donc c et d sont tous deux non nuls. Tout diviseur commun à c et à d est diviseur commun à a et à b, donc c et d sont premiers entre eux car a et b le sont. Si c et d sont de même parité, alors a et b sont tous les deux pairs, ce qui n'est pas le cas, donc c et d sont de parités différentes. Cinq divise b donc il ne divise pas a et donc il ne divise pas c.