Entier de Dirichlet - Définition

Equation de Pell-Fermat

Équation

L'objectif est de résoudre l'équation suivante :

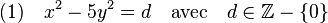
Dans un premier temps, l'objectif est de se ramener à une équation utilisant l'expression de la norme dans l'anneau des entiers de Dirichlet. Un changement de variable permet d'écrire la solution de la manière suivante :

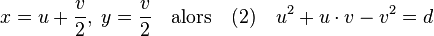
Pour une raison de simplicité, on appelle solution de l'équation (2) tout entier de Dirichlet de norme égale à d. En effet, dire qu'un entier de Dirichlet a + b.ω est de norme d revient à dire que a² + a.b - b² = d. Cette remarque, ainsi que la connaissance de la structure des nombres premiers de Dirichlet permet de venir à bout de l'équation (1).

Le facteur 1/2, introduit par le changement de variables, doit être pris en compte. Une proposition intermédiaire est nécessaire :

• S'il existe un entier de Dirichlet de norme égale à d en valeur absolue, alors il existe un entier de Dirichlet de la forme a + 2b.ω de norme d en valeur absolue et le couple (a - b, b) est une solution de l'équation (1) pour le paramètre ±d. Ici a et b désigne deux entiers relatifs.

Soit a₁ + b₁.ω un entier de Dirichlet de norme égale à d en valeur absolue. Si b₁ est pair la proposition est bien vérifiée. Sinon, deux cas se présentent, selon la parité de a₁. Si a₁ est impair, on remarque que ω est une unité, donc ω.(a₁ + b₁.ω) est de norme égale à d en valeur absolue. L'égalité ω.(a₁ + b₁.ω) = b₁ + (a₁ + b₁).ω et le fait que a₁ et b₁ soient impairs permet de conclure. Si a₁ est pair, appliquons le même raisonnement avec 1 + ω, on obtient l'égalité suivante : (1 + ω).(a₁ + b₁).ω = a₁ + b₁ + (a₁ + 2b₁).ω. Cette dernière égalité, ainsi que le fait que a₁ soit pair permet encore de conclure. Pour terminer la démonstration, il suffit de remarquer que le couple (a - b, b) est effectivement une solution de l'équation (1).

Enfin si (a, b) est une solution, alors (±a, ±b) est aussi une solution. Pour cette raison, ne sont cherchées uniquement les solutions tel que a et b sont positifs.

La valeur absolue de d est égale à un

Résoudre l'équation (2) dans le cas où le paramètre est égal à ±1 est possible avec la connaissance du groupe des unités. Toutes les unités sont connues, elles sont de la forme ±ωⁿ où n est un entier relatif et le signe de la norme est celui de (-1)ⁿ. Enfin, la suite de Fibonacci donne les coordonnées exactes des unités.

En revanche, les solutions recherchées sont celles qui ont pour coefficients b un entier pair. Une récurrence permet d'établir que, si (a_n) désigne la suite de Fibonacci déjà utilisée, a_n est pair si et seulement si n est congru à 1 modulo 3. L'article Entier algébrique étudie cette configuration pour toutes les équations de Pell-Fermat. Cela permet de conclure que :

• L'ensemble des solutions S₁ de l'équation (1) pour le paramètre d égal à 1 est :

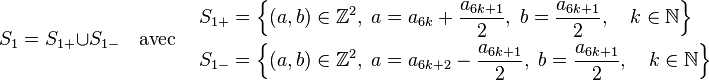
• L'ensemble des solutions S_-1 de l'équation (1) pour le paramètre d égal à -1 est :

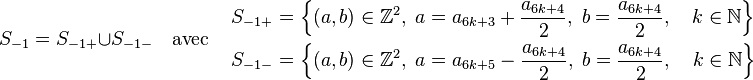
La valeur absolue de d est égale à un nombre premier p

L'analyse des nombres premiers de Dirichlet permet de résoudre la question. La lettre p désigne ici un entier naturel premier.

• Si p est congru à 2 ou à 3 modulo 5, alors l'équation (1) n'admet pas de solution pour le paramètre ±p.

En effet, L'équation (2) n'a pas de solution car il n'existe aucune norme dans Z[ω] égale à ±p et toute solution de l'équation (1) se construit à l'aide d'une solution de l'équation (2).

• Si p est congru à 1 ou à 4 modulo 5, alors l'équation (1) admet une infinité de solutions pour les deux paramètres p et -p.

Si p est congru à 1 ou à 4, il existe un nombre premier π ayant pour norme p. Quitte à multiplier π par ω ou ω², il est possible de construire une solution (a, b) à de l'équation (2) tel que b soit pair. Multiplier cette solution par les éléments de S₁ d'un côté et par S_-1 de l'autre fournit une infinité de solutions pour chacun des deux paramètres p et -p. L'article équation de Pell-Fermat montre qu'il n'y en a pas d'autres.

Cas général

Le cas général est analogue à celui des équations de type x² ± n.y² = d, il est traité en détail dans l'article Théorème des deux carrés de Fermat. Il prend la forme suivante :

• S'il existe un exposant d'un entier naturel premier congru à 2 ou à 3 modulo 5 dans la décomposition en facteurs premiers de d alors l'équation (1) n'a pas de solution.

On raisonne par contraposé, c'est-à-dire que l'on suppose que l'équation (1) admet une solution pour d et on montre que les exposants des facteurs premiers de d congru à 2 ou 3 modulo 5 sont pairs.

Soit (a, b) une solution de l'équation (1), α = a - 2b + 2b.ω est de norme d. Considérons la décomposition en facteurs premiers de Dirichlet de α. Le paragraphe précédent montre que la norme d'un nombre premier de Dirichlet est, soit en valeur absolue égale au carré d'un entier naturel premier congru à 2 ou à 3 modulo 5, soit à un entier naturel premier congru à 1 ou à 4 modulo 5 ou encore à 5. L'exposant des facteurs premiers de la norme de α congru à 2 ou à 3 est en conséquence toujours pair car la décomposition en facteurs premiers est unique. On en déduit que la décomposition en facteurs premiers de d ne contient pas d'exposant impair pour les facteurs premiers congru à 2 ou à 3 modulo 5. Ce qui termine la démonstration.

• Si d ne contient aucun exposant impair pour les entiers naturels premiers congru à 2 ou à 3 modulo 5 présents dans sa décomposition en facteurs premiers, alors l'équation (1) admet une solution pour les deux paramètres d et -d.

Si d vérifie l'hypothèse de la proposition, il existe une suite finie de nombres premiers p_i congru à 2 ou à 3 modulo 5, une suite de nombres premiers (q _j) non congru à 2 ou à 3 modulo 5 et deux suites à valeur dans les entiers strictement positifs (n_i) et (m_j) telles que :

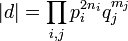
L'analyse des nombres premiers de Dirichlet montre l'existence d'entiers α_j tels que leurs normes vérifient les égalités suivantes :

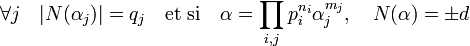
A partir de là, on raisonne comme pour le cas où d est premier et on construit deux suites infinies de solutions, une pour la valeur d et l'autre pour la valeur -d. On remarque qu'il existe deux solutions différentes pour une norme égale à q _j, soit α_j² soit q _j. La combinatoire de toutes les écritures d'un nombre de norme d, donne l'intégralité des solutions, une fois composées avec les ensembles S₁ et S_-1.