Entier de Dirichlet - Définition
La liste des auteurs de cet article est disponible ici.
Nombres premiers
Définitions et exemples
Un peu de vocabulaire est utile :
-
- Un nombre premier p dans l'ensemble des entiers naturels est dit inerte si et seulement si, il est premier en tant qu'entier de Dirichlet.
-
- Un entier de Dirichlet α est dit irréductible si et seulement si, il existe une unité ε et un nombre premier de Dirichlet π tel que α soit égal à ε.π.
Autrement dit, un entier de Dirichlet est dit irréductible s'il est différent d'une unité et s'il n'admet comme diviseur que lui-même et 1 à un facteur unité près.
L'entier √5 est un entier de Dirichlet irréductible. On remarque en effet que la norme de √5 est égal à -5 égal, en valeur absolue, à un nombre premier dans les entiers naturels. On dispose en effet de la propriété suivante :
-
- Un entier de Dirichlet ayant une norme en valeur absolue égale à un nombre premier est irréductible.
La valeur 2 est un nombre premier de Dirichlet, même si sa norme n'est pas irréductible. Il suffit pour cela de montrer qu'il n'existe pas d'entier de Dirichlet dont la norme est égale à deux. Tout diviseur de deux possède pour norme égale en valeur absolue soit à 1 soit à 4 (c’est-à-dire la norme de deux). Montrons, par l'absurde qu'il n'existe pas d'entier de Dirichlet de norme égal à ±2. Supposons qu'un tel nombre existe et soit a et b les deux entiers relatifs de même parité tel que 1/2(a + b.√5) soit égal à ce nombre. Sa norme est égale à deux, donc a2 + 5.b2 = ±8. Si a et b sont pairs, alors il existe deux entiers u et v tel que a = 2.u et b = 2.v, l'équation devient u2 + 5.v2 = ±2, une analyse modulo quatre montre que le premier terme ne peut jamais être congru à deux, d'où une contradiction si a et b sont pairs. Si a et b sont impairs, alors il existe u et v tel que a = 2.u + 1 et b = 2.v + 1, l'équation devient en simplifiant par 4 : u.(u + 1) - 5.v.(v+ 1) - 1 = ±2, le premier terme est impair le second pair, d'où une contradiction si a et b sont impairs.
Des raisonnements de cette nature permettent de trancher au cas par cas pour savoir si un entier de Dirichlet est irréductible ou non. Une méthode plus générale est nécessaire pour établir la géographie des nombres premiers.
Résidu quadratique
La démonstration du petit théorème de Fermat établit des différences de nature entre les nombres premiers de N. Certains sont cassés dans l'arithmétique de Dirichlet, d'autres non. Pour établir la géographie des nombres premiers de Dirichlet, il est nécessaire de savoir lesquels résistent ainsi que ceux qui se brisent. Cette question est liée à l'équation diophantienne suivante, si p désigne un nombre premier de N :
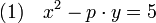
Elle fut résolue dans le cas général par Gauss qui appela le théorème associé, théorème d'or. Il est maintenant plus connu sous le nom de Loi de réciprocité quadratique. Résoudre cette équation revient à déterminer si 5 est ou non le reste d'une division euclidienne d'un carré parfait par p, un nombre premier. On dit alors que 5 est un résidu quadratique modulo p. Le petit théorème de Fermat permet de montrer que :
-
- Le nombre 5 est le reste d'une division euclidienne d'un carré parfait par un nombre premier p différent de 5 si et seulement si p est congru à ±1 modulo 5.
La relation entre l'équation (1) et la nature des nombres premiers est donnée par la proposition suivante :
-
- Un nombre premier p de N différent de 2 est inerte, si et seulement si, 5 n'est pas un résidu quadratique modulo p.
Résoudre cette équation permet d'établir des résultats un peu inattendus, connu sous le nom de Loi d'apparition des nombres premiers au sein de la suite Fibonacci. Si (an) désigne la suite de Fibonacci :
-
- Si p est un nombre premier de N différent de 5 et décomposé, alors ap est un multiple de p ainsi que ap-1 - 1.
Les démonstrations se fondent sur les propriétés géométriques du nombre d'or ainsi que le petit théorème de Fermat. Une propriété du nombre d'or est d'intervenir dans la construction à la règle et au compas du pentagone régulier. Si les sommets du polygone sont vus comme des points du plan complexe, ils sont racines du polynôme X5 - 1 = 0. Le petit théorème de Fermat indique lui que, dans le monde des congruences modulo π, tout résidu est solution de l'équation Xp2-1 - 1 ≡ 0 mod p, si p désigne la valeur absolue de la norme de π. L'analogie est suffisante. La preuve se résume à montrer qu'un nombre premier p différent de 5 n'est pas irréductible dans les entiers de Dirichlet si et seulement si, p2 - 1 est un multiple de 5.
Une fois encore, l'usage d'outils sophistiqués permet des démonstrations plus rapides pour des résultats plus généraux. Ici, l'outil clé est la loi de réciprocité quadratique. Elle se démontre, par exemple avec les corps finis ou les groupes abéliens finis et particulièrement leur analyse harmonique. Les démonstrations proposées ici se cantonnent aux outils de l'arithmétique élémentaire.
Montrons dans un premier temps l'équivalence entre l'existence d'une solution à l'équation diophantienne et le fait que p soit décomposé.
-
- Un nombre premier p de N différent de 2 est inerte, si et seulement si, 5 n'est pas un résidu quadratique modulo p :
- Traitons tout d'abord le cas où p est égal à 5. Il n'est pas premier dans Z[ω] car √5 le divise et il est bien un résidu quadratique car 02 et 5 ont même reste par la division euclidienne par 5.
- Le principe de la démonstration pour les autres cas se fonde sur une propriété établie pour prouver le petit théorème de Fermat. Un nombre premier p est inerte si et seulement si ω n'est congru à aucun entier compris entre 0 et p - 1 modulo π, ici π désigne un facteur premier de p. Si p est premier, π et p sont confondus à un facteur unité près, sinon π divise strictement p. Si p n'est pas premier, tout entier de Dirichlet est congru à un entier compris entre 0 et p - 1 modulo π (cf paragraphe précédent). En revanche, si p est premier, aucun point a + b.ω avec a compris 0 entre p - 1 et b compris entre 1 et p - 1 n'est congru à un entier compris entre 0 et p - 1 modulo p et donc modulo π.
- Supposons que ω soit congru à un entier w modulo π et montrons que 5 est un résidu quadratique modulo p. Le nombre 4(ω2 - ω - 1) est égal à 0, donc 4w2 - 4w - 4 congru à 0 modulo π ou encore, est un multiple de π. Ceci montre que 4w2 - 4w + 1 - 5, égal à (2w - 1)2 - 5, est un multiple de π, en conséquence (2w - 1)2 est un carré parfait congru à 5 modulo π. Le conjugué de (2w - 1)2 - 5, égal à lui même est un multiple de φ(π). La décomposition en facteurs premiers de (2w - 1)2 - 5 contient à la fois π et φ(π), ce qui permet de conclure que (2w - 1)2 - 5 est un multiple de p dans Z[ω]. Il existe un entier de Dirichlet q tel que p.q est égal à (2w - 1)2 - 5. Comme (2w - 1)2 - 5 et p sont entiers relatifs, q l'est nécessairement. On a montré l'existence d'un carré parfait c2 tel que c2 - 5 est un multiple de p dans N, 5 est bien un résidu quadratique modulo p.
- Réciproquement, supposons que c soit un résidu quadratique de 5 modulo p et montrons que ω est congru à un entier modulo π. L'identité de Bézout montre l'existence d'un entier d tel que 2.d est congru à 1 modulo π car π est premier de Dirichlet, 2 et π sont premiers entre eux. L'entier 2.d(1 + c) vu comme un entier de Dirichlet est congru à 2.ω modulo π et donc l'entier d(1 + c) est congru à ω. La division euclidienne de d(1 + c) par p montre l'existence un entier naturel compris entre 0 et p - 1 congru à d(1 + c) modulo p et donc modulo π. Le fait que ω soit congru à un entier compris entre 0 et p - 1 modulo π montre que p n'est pas irréductible et termine la démonstration.
Etudions le cas simple, c'est-à-dire celui où p est congru à 2 ou à 3 modulo 5. Un rapide calcul montre que p n'est pas décomposable.
-
- Soit p un nombre premier de N. Si p est congru à 2 ou à 3 modulo 5, p est inerte et 5 n'est pas un résidu quadratique modulo p :
- Supposons que p soit un nombre premier décomposable, il existe un entier de Dirichlet a + b.ω de norme égale à p. Cette norme est égale à a2 + a.b - b2, calculons sa congruence modulo 5 :
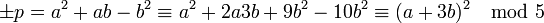
- Un carré parfait modulo 5 n'est jamais congru à 2 ou à 3, en conséquence, si p est n'est pas décomposable s'il est congru à 2 ou à 3 modulo 5. La proposition précédente montre qu'alors 5 n'est pas un résidu quadratique.
L'étape d'après consiste à utiliser la propriété géométrique du nombre d'or. Un pentagone se définit aussi comme les racines du polynôme cyclotomique X5 - 1. Une méthode relativement simple pour une équation d'un degré aussi élevé permet de venir à bout de l'extraction de racine. La première étape voit l'apparition d'une valeur formellement proche du nombre d'or, ce qui permet d'établir la proposition suivante :
-
- Soit p un nombre premier de N différent de 2 et de 5 et π un nombre premier divisant p. S'il existe un entier de Dirichlet α non congru à 1 modulo π tel que α5 - 1 soit un multiple de π, alors l'entier p est décomposé :
- Pour la démonstration, on utilise l'égalité suivante :
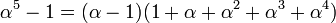
- Supposons que α5 - 1 soit multiple de π et montrons que p est décomposable dans les entiers de Dirichlet. Le lemme d'Euclide assure que l'un des deux facteurs de l'égalité précédente est un multiple de π. Par hypothèse, ce n'est pas le premier, c'est donc le dernier. On obtient :
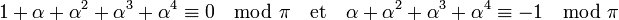
- En multipliant la première égalité par α on remarque que α5 est congru à -α - α2 - α3 - α4 donc à 1 modulo π d'après la deuxième égalité. Si u désigne α + α4 et v α2 + α3, comme α5 est congru à 1 modulo π :
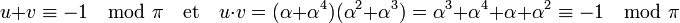
- En multipliant u + v par u :
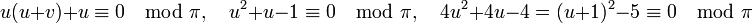
- Il existe un entier congru à 5 modulo π ce même entier est aussi congru à φ(π) donc au produit car ces deux entiers de Dirichlet sont premiers et 5 est congru à un carré parfait modulo p. Le fait que 5 soit un résidu quadratique ainsi que la proposition précédente, permet de conclure.
Il est temps d'utiliser le petit théorème de Fermat, si p est irréductible l'exposant du petit théorème de Fermat est égal à p2 - 1 un multiple de 5 si p est congru à 1 ou à 4 modulo 5. Le petit théorème de Fermat traite d'un polynôme multiple de X5 - 1, l'aide de la proposition précédente permet de conclure.
-
- Si p est un nombre premier congru à 1 ou à 4 modulo 5, p est décomposé :
- Raisonnons par l'absurde et supposons que p soit congru à 1 ou à 4 modulo p et irréductible dans les entiers de Dirichlet. Un simple calcul montre que p2 - 1 est un multiple de 5. On note k l'entier tel que 5.k est égal p2 - 1. Soit α un entier de Dirichlet non multiple de p et n le plus petit entier tel que αn - 1 soit un multiple de p. Le petit théorème de Fermat nous indique que n est un diviseur de p2 - 1. La proposition précédente montre que n n'est pas un multiple de 5, sinon αn/5 serait un entier non congru à 1 modulo p tel que, à la puissance 5, il serait congru à 1 modulo p. L'existence d'un tel entier montre que 5 est un résidu quadratique modulo p et que p est décomposable. On en déduit que n est un diviseur de k. Ceci montre que pour tout entier de Dirichlet α non multiple de p, αk - 1 est un multiple de p.
- Soient k entiers de Dirichlet α1, α2, ..., αk non multiple de p et tous de congruences différentes modulo p. Il en existe toujours, le paragraphe précédent montre qu'il existe exactement p2 - 1 congruences différentes modulo p et k est strictement plus petit que p2 - 1. Le polynôme Xk - 1 annule la congruence de α1, ce qui montre l'existence d'un polynôme P1(X) de degré k - 1 tel que :
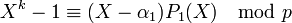
- L'entier de Dirichlet α2k - 1 est un multiple de p, donc (α1 - α2)P1(α2) est aussi un multiple de p. Par construction des αj, α1 - α2 n'est pas un multiple de p. Le lemme d'Euclide montre que P1(α2) est un multiple de p. Ceci montre l'existence d'un polynôme P2(X) tel que :
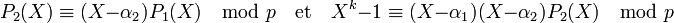
- En continuant le même raisonnement jusqu'à k on obtient la congruence :
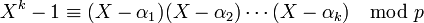
- Considérons alors un entier de Dirichlet α non multiple de p et congru à aucun des éléments α1, α2, ..., αk. On a vu que αk - 1 est un multiple de p, donc :
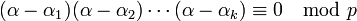
- Le terme précédent est un multiple de p, pourtant aucun des facteurs α - αj n'est un multiple de k. Cette assertion contredit le lemme d'Euclide et ne peut être juste. En conséquence l'hypothèse p est irréductible dans les entiers de Dirichlet est fausse, ce qui démontre la proposition.
-
- Si p est un nombre premier de N différent de 5 et décomposé, alors ap est un multiple de p ainsi que ap-1 - 1 :
- La démonstration est rapide avec le petit théorème de Fermat. Le nombre p admet d'après les deux propositions précédentes deux nombre premiers π et φ(π) dans sa décomposition en facteurs premiers. La norme de chacun des nombres premiers de Dirichlet est p. Le petit théorème de Fermat affirme que ωp-1 - 1 est un multiple de π et de φ(π) donc de p. L'analyse de la suite de Fibonacci montre que ωp-1 - 1 = ap-1 - 1 + ap.ω, ce qui démontre le résultat. Une vérification manuelle montre que a11 est égal à 55, a10 à 33 + 1, a19 à 2585 = 19x136 et a18 à 19x84 + 1.