Entier de Dirichlet - Définition

Groupe des unités

Norme

Les unités, c'est-à-dire l'ensemble des éléments inversibles pour la multiplication, forment un groupe commutatif pour la multiplication. Dans le cas des entiers de Dirichlet, ce groupe est vaste, ce qui constitue une obstruction. En effet, ces éléments ne sont pas traitables avec les outils classiques de l'arithmétique, avec eux, pas d'identité de Bézout, ni de lemme d'Euclide, de décomposition en facteurs premiers ou de petit théorème de Fermat. En conséquence, il est nécessaire de bien comprendre la structure de ce groupe pour pouvoir le manier sans trop de difficultés. La norme est utile.

Le groupe des unités de l'anneau de Dirichlet est composé des éléments de norme égale à ±1.

En effet, si ε est un entier de Dirichlet de norme égal à ±1, alors soit φ(ε) soit -φ(ε) est l'inverse de ε, ce qui montre que ε est bien une unité. Réciproquement si ε est une unité, alors :

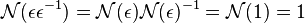
La norme de ε est un entier relatif inversible, il n'en existe que deux, 1 et -1, ce qui montre la réciproque.

Déterminer le groupe des unités revient à résoudre l'équation suivante :

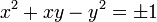
Cette équation diophantienne, qui intervient souvent dans l'étude des entiers de Dirichlet, correspond à l'expression, en termes de coordonnées, de la norme d'un entier de Dirichlet. La suite de l'article montre qu'elle est équivalente à une équation de Pell-Fermat.

Puissance du nombre d'or

Un exemple d'unité est donné par ω, on vérifie de fait que N(ω) = 0 + 0 - 1² = -1. La compatibilité de la norme avec la multiplication montre que si n est un entier relatif, ±ωⁿ est aussi une unité car :

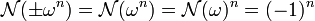
• Soit e un entier égal à 1 ou à -1 et n un entier relatif, eωⁿ est une unité de l'anneau des entiers de Dirichlet.

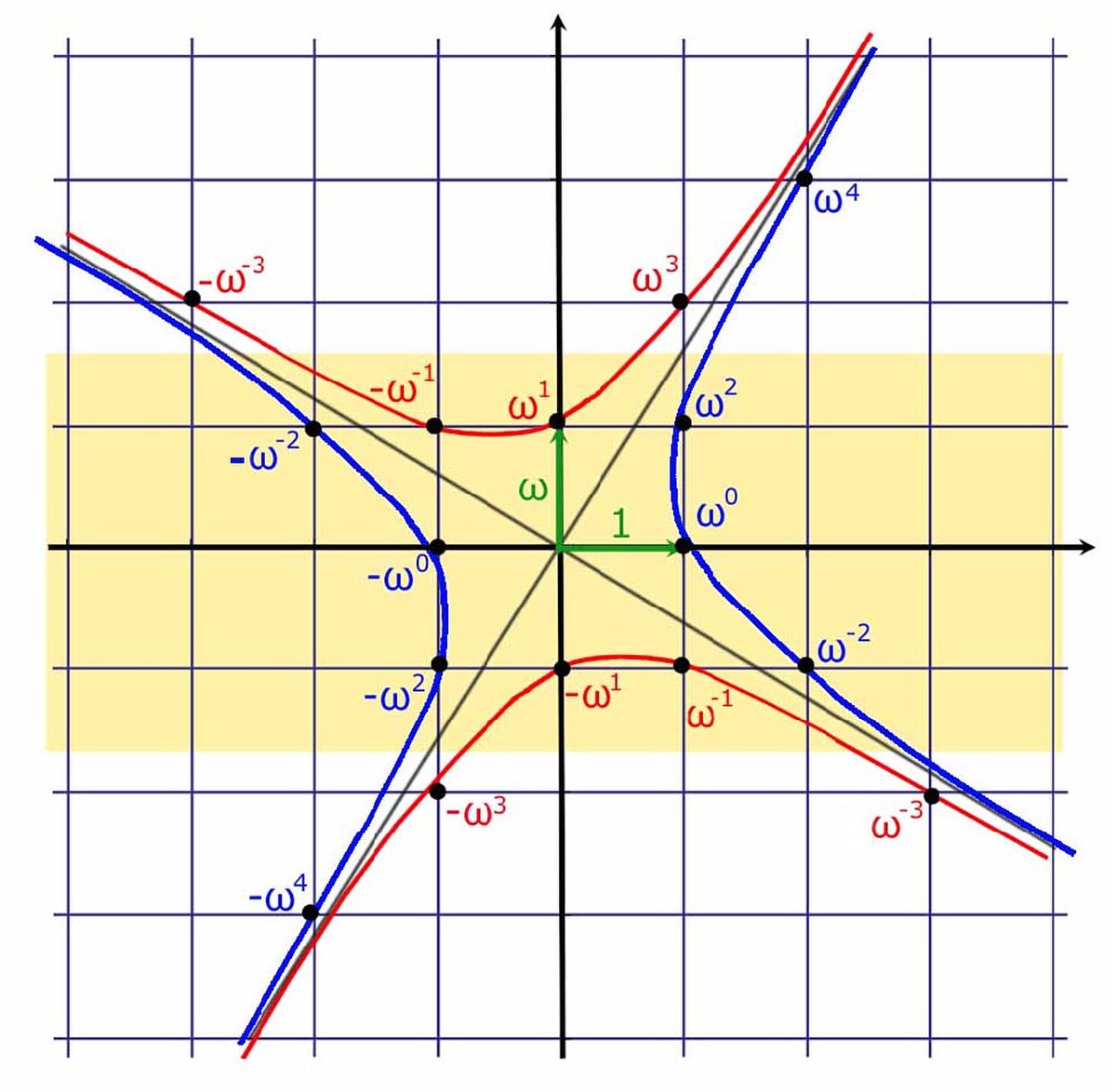
La figure de droite illustre le positionnement des unités, les branches bleues supportent les unités positives et les rouges, les négatives. Cette méthode, purement algébrique, pour déterminer les unités est généralisable. Brahmagupta l'avait remarqué, ce qui lui a permis de construire une méthode très générale sur ce principe, appelée méthode chakravala.

Une question plus délicate est celle de la réciproque, la réponse est donnée par la proposition suivante :

• Soit ε un élément du groupe des unités, il existe un entier e égal à 1 ou -1 et un entier relatif n tel que ε soit égal à eωⁿ.

Cette question arrêta longuement les mathématiciens dans le cas général. C'est Joseph-Louis Lagrange qui finalement vient à bout du cas des entiers quadratiques en prolongeant les travaux d'Euler sur la fraction continue d'un nombre quadratique. Dirichlet trouve au siècle suivant une méthode de résolution valable pour tous les entiers algébriques, généralisant ainsi les travaux de Lagrange. Ce résultat est l'objet d'un théorème dit des unités de Dirichlet. Une démonstration simplifiée, pour résoudre uniquement le cas des entiers quadratiques, est proposé dans l'article Entier quadratique. Si l'objectif n'est que l'étude du groupe des unités des entiers de Dirichlet, une démonstration élémentaire est envisageable.

Soit ε = a + b.ω une unité de l'anneau. L'objectif est de montrer que, au signe près, ε est une puissance de ω. Si b est égal à 0 ou à 1, il existe exactement dix solutions qui se traitent manuellement. Ils correspondent aux dix solutions dans la bande orange de la figure.

Sinon, quatre cas se présentent, a et b positifs, a positif et b négatif, a négatif et b positif et enfin a et b négatif. Ces quatre cas correspondent aux huit branches asymptotiques des deux hyperboles de la figure qui se groupent deux à deux. Ils se traitent tous de manière analogue. Considérons donc le cas où a et b sont positifs et b est supérieur ou égal à deux.

Montrons que a < b < 2.a. Si b est plus petit ou égal à a alors N(a + b.ω) est plus grand que a² (et donc plus grand que 4), ce qui est impossible.

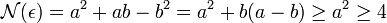
Si b est plus grand que 2.a alors N(a + b.ω) est plus petit que -a², ce qui est tout aussi impossible.

Donc (a + b.ω).ω ^-1 = a₁ + b₁ω est aussi un élément du groupe de l'unité du même quadrant. En effet b₁ est égal à a et a₁ à b - a. Les deux coefficients sont strictement positifs et b₁ strictement plus petit que b. En réitérant le processus de multiplication par ω ^-1, on obtient finalement un élément du groupe de l'unité dont le coefficient de ω est soit zéro soit un. Un tel élément est égal à une puissance de ω à un facteur ±1. Ceci montre que ε est bien une puissance de ω.

 

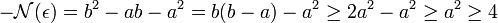
Suite de Fibonacci

Si l'on considère la suite des coordonnées de ωⁿ pour n un entier naturel, on obtient (1,0), (0,1), (1,1), (1,2), (2,3) ... On reconnait là une suite de Fibonacci :

• Soit (a_n) une suite à valeur dans les entiers naturels définie par la relation de récurrence suivante :

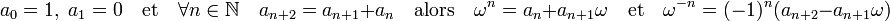
Cette proposition se démontre par récurrence, un rapide calcul montre que la formule est vraie si n est égal à 0 ou 1, supposons la première formule vraie jusqu'à n :

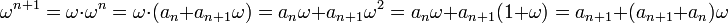
Une démonstration de même nature établit la relation de récurrence pour les valeurs négatives de n.