Entier de Dirichlet - Définition
La liste des auteurs de cet article est disponible ici.
Division euclidienne
Existence
La norme possède une propriété importante, elle permet de définir une division euclidienne. Cette norme n'est pas toujours positive. Le stathme v, c’est-à-dire la fonction permettant de définir la division et égale à la valeur absolue dans le cas des entiers relatifs, ne doit prendre que des valeurs positives. Pour cette raison, on le choisit égal la valeur absolue de la norme. Cette application est encore multiplicative, c’est-à-dire que si α et β sont deux entiers de Dirichlet, alors : v(α.β) = v(α).v(β).
-
- Soit α et β deux entiers de Dirichlet tel que β soit non nul, il existe un couple d'entiers de Dirichlet (θ,ρ) tel que :
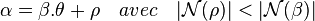
La démonstration est analogue à celle des entiers de Gauss. Considérons la fraction rationnelle α/β et l'ensemble des éléments ζ de Q[√5] tel que |N(α/β - ζ)| soit strictement inférieur à un. Cet ensemble correspond à la zone bleue de la figure de droite, délimitée par les quatre branches des hyperboles. L'intersection de cette zone avec les entiers de Dirichlet, correspondant aux points du réseau, sont les candidats à être les quotients de la division euclidienne. Ces candidats sont illustrés par un petit cercle sur la figure. Le carré, illustré en orange, de côté 1 et de centre α/β est strictement inclus dans la zone bleue. Il contient au moins un point θ, illustré ici en rouge. Ce point θ vérifie :
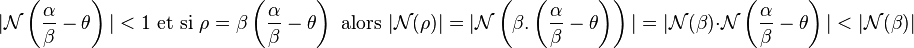
Ceci montre qu'il existe une division euclidienne dans l'anneau des entiers de Dirichlet. Elle possède un aspect un peu déroutant, il n'existe pas un reste possible, mais jusqu'à une infinité. Le nombre de restes possibles est en effet lié au groupe des unités, si ρ1 et ρ2 sont deux restes possibles, il existe une unité ε tel que ρ2 = ερ1. Cette situation est finalement la même que pour les entiers relatifs ou il existe parfois deux restes possibles (cf division euclidienne).
Conséquences
Comme cet anneau est euclidien, il est principal, l'identité de Bézout s'applique ainsi que le lemme d'Euclide et le théorème fondamental de l'arithmétique. L'article Entier de Gauss propose des démonstrations directement applicables au cas traité ici. Les démonstrations sont très proches de celles de l'arithmétique usuelle. Montrons-le, par exemple, pour le lemme d'Euclide. Il indique que si α, β et γ sont trois entiers de Dirichlet tels que α divise le produit β.γ et tel que α et β soient premiers entre eux, alors α divise γ. Avec ces hypothèses et l'identité de Bézout, comme α et β sont premiers entre eux, il existe deux entiers de Dirichlet ρ et θ tels que α.ρ + β.θ = 1, on multiplie membre à membre par γ, on obtient α.ρ.γ + β.θ.γ = γ. Comme β.γ est un multiple de α, il existe un entier de Dirichlet δ tel que β.γ soit égal à α.δ. En remplaçant β.γ par α.δ, on obtient α(ρ.γ + θ.δ) = γ, ce qui démontre la proposition.
Cette démonstration est, à la modification près sur le terme d'entier qui devient entier de Dirichlet, exactement la même que celle du cas des entiers relatifs. Cette logique, qu'Euler tente d'appliquer, nécessite l'existence d'une division euclidienne, ce que Gauss a compris.
Petit théorème de Fermat
Si l'analogie est profonde, elle doit néanmoins être maniée avec précaution. Le petit théorème de Fermat, l'un des piliers de l'arithmétique élémentaire, s'exprime par exemple de manière un peu différente :
-
- Soient π un nombre premier de Dirichlet, α un nombre entier de Dirichlet qui n'est pas un multiple de π et n un entier strictement positif égal à la valeur absolue de la norme de π, alors αn-1 - 1 est un multiple de π.
En utilisant le langage des congruences, on obtient l'égalité suivante, caractéristique du petit théorème de Fermat :
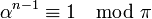
La démonstration proposée ici ne fait appel ni à la théorie des groupes ni aux techniques plus sophistiquées comme celle de l'anneau quotient ou des corps finis. Les démonstrations de l'article Entier quadratique, faisant usage d'outils plus puissants arrivent à des conclusions plus générales avec des démonstrations plus succinctes.
La démonstration est un plus longue que celle, plus usuelle des entiers naturels. Les nombres premiers ne sont, dans le cas étudié ici, pas tous de même nature, comme le montre la proposition suivante. Le terme π désigne un nombre premier de Dirichlet :
-
- Soit π est un élément de N, soit la norme de π est, en valeur absolue, un nombre premier dans l'ensemble N des entiers naturels :
- Le raisonnement est le suivant, on suppose que |N(π)| n'est pas un nombre premier dans les entiers naturels et on montre que π est un nombre premier dans N.
- L'entier naturel |N(π)| n'est pas premier dans N par hypothèse, il admet deux diviseurs n et m dans N, chacun différent de 1. Soit β un nombre premier de Dirichlet présent dans la décomposition en facteurs premiers de n. Il est en effet possible de considérer n comme un entier de Dirichlet. Soit γ un entier de Dirichlet tel que β.γ soit égal n. Ce nombre β divise N(α) c'est-à-dire le produit de α et de son conjugué. Comme β est premier, le lemme d'Euclide, appliqué dans Z[ω], montre que β divise soit α soit son conjugué. Comme α et son conjugué sont des nombres premiers de Dirichet, β est égal soit à α soit à son conjugué. La norme N(α) est égale au produit de α et de son conjugué, on en déduit que γ.n est égal à soit à α soit à son conjugué. Comme α et son conjugué sont premiers de Dirichlet et que m n'est pas une unité par hypothèse, γ est égal à 1.
- Or β est un nombre premier de Dirichlet, donc β.γ = n est un nombre premier, c'est-à-dire divisible seulement par lui-même ou par 1, à un facteur unité près. L'entier n divise le produit de α et de son conjugué, il divise l'un des deux. Comme ces deux nombres sont premiers de Dirichlet, il est égal à l'un des deux, à un facteur unité près. Si π ou son conjugué est égal à n, à un facteur unité près, alors π, tout comme son conjugué sont égaux à n. Ceci montre que le nombre premier de Dirichlet π est élément de N. Comme π est premier de Dirichlet, il est aussi premier dans N, ce qui termine la démonstration.
Étudions, dans un premier temps, le cas d'un nombre premier de Dirichlet π dont la norme n est en valeur absolue un nombre premier dans les entiers naturels. Un exemple est donné par 3 + 2.ω. Il vérifie l'égalité :
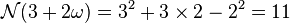
Si deux entiers de Dirichlet ont un produit égal à 3 + 2.ω, le produit de leur norme est égal à 11. Comme 11 est un nombre premier dans N, une des normes est égale à ±1, ce qui montre que l'entier de Dirichlet associé est une unité et donc que 3 + 2.ω n'admet pas de diviseur propre.
-
- Si π est un nombre premier dont la norme n est, en valeur absolue, un nombre premier dans N, alors le petit théorème de Fermat est vérifié :
- Le raisonnement utilisé consiste à se ramener à un cas où la formulation usuelle du petit théorème de Fermat s'applique. Soient p1, p2, a et b les quatre entiers relatifs tels que π = p1 + p2.ω soit égal à π et a + b.ω à α. Les entiers relatifs p2 et n sont premiers entre eux, sinon p2 serait un multiple de n d'après la formule exprimant la norme d'un entier de Dirichlet, en fonction de ses coordonnées. L'identité de Bézout montre l'existence de deux entiers g et h tel que p2.g + n.h = -b. On en déduit que α + g.π + h.n est un entier relatif. De plus n est égal à π.φ(π) donc :
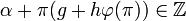
- Ce qui signifie que α est congru à un entier relatif modulo π. Notons c cet entier relatif, comme α est congru à c modulo π, αn-1 est congru cn-1 modulo π. Le petit théorème de Fermat permet d'affirmer que cn-1 est congru à 1 modulo n donc αn-1 est congru à 1 modulo n et donc aussi aux diviseurs de n comme π. Ce qui termine la démonstration.
Il reste le deuxième cas à traiter, celui où π est à la fois un nombre premier de Dirichlet et un entier naturel. L'entier π est aussi un nombre premier dans les entiers naturels. En effet, il n'admet pas de diviseur autre qu'une unité et lui-même, à un facteur unité près, dans les entiers de Dirichlet et donc a fortiori dans N. L'objectif est alors de montrer que pour tout α, non multiple de π, la congruence suivante est vérifiée :
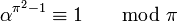
-
- Si π est un nombre premier de N premier dans l'anneau des entiers de Dirichlet, alors α2π -1 est congru à 1 modulo π :
- La configuration est suffisamment différente pour devoir reprendre pas à pas la démonstration du petit théorème de Fermat. Soit C l'ensemble des entiers non nuls de Dirichlet c + d.ω tel que les coordonnées c et d se situent dans l'intervalle [0, p-1]. L'ensemble C forme une espèce de carré et contient exactement π2 - 1 points. Le -1 correspond au zéro que l'on a retranché de l'ensemble.
-
- Un élément β de l'anneau des entiers de Dirichlet, non multiple de π, est congru à un et un seul élément de C modulo π.
- On note β = aβ + bβ.ω. Les divisions euclidiennes dans l'ensemble des entiers relatifs (avec un reste toujours positif) de aβ et de bβ montrent qu'il existe un représentant de β dans C, en effet :
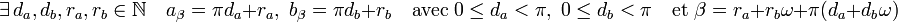
- On note βc = ra + rb.ω, βc est congru à β modulo π et est élément de C. Réciproquement, la différence entre deux éléments de C ne contient que des points aux coordonnées inférieures à π en valeur absolue, pour que cette différence soit un multiple de π, il faut qu'elle soit nulle. Ce qui montre l'unicité du représentant βc de β dans C.
Soit ψ l'application de C dans C qui à β, un élément de C, associe le représentant de α.β dans C.
-
- L'application ψ est une bijection.
- Soit β1 et β2 deux éléments de C ayant même image par ψ. La différence ψ(β1) - ψ(β2) est nulle, ce qui signifie que α.(β1 - β2) est un multiple de π. Comme π est premier en tant qu'entier de Dirichlet, il divise soit α, soit β1 - β2. Par hypothèse π ne divise pas α, il divise donc β1 - β2. La proposition précédente montre que cela signifie que β1 et β2 sont égaux, c'est-à-dire que ψ est injective. Toute application injective d'un ensemble fini dans lui même est une surjection, le caractère bijectif de ψ est ainsi démontré.
On désigne par Πc le produit de tous les éléments de C. Cette valeur est l'équivalent du terme (π-1)! dans la démonstration élémentaire de l'article Petit théorème de Fermat.
-
- L'entier de Dirichlet Πc.απ2-1 est congru à Πc modulo π.
- Il suffit de remarquer que Πc est le produit d'exactement les π2 - 1 éléments de C. Comme ψ est une bijection il correspond aussi au produit des π2 - 1 éléments ψ(β) si β décrit C. Or ce produit est congru à Πc.απ2-1 modulo π car dans le monde des congruences, ψ correspond à une multiplication par α. Ceci montre que Πc.απ2-1 est congru à Πc modulo π.
-
- Conclusion
- Le paragraphe précédent montre que Πc(απ2-1 - 1) est un multiple de π. Aucun élément constituant le produit Πc n'est un multiple de π, la contraposée du lemme d'Euclide permet de conclure que π ne divise pas Πc. Si π ne divise par Πc une nouvelle application de ce même lemme montre que π divise l'autre facteur : αp2-1 - 1. Dire que π divise απ2-1 - 1 est exactement équivalent au petit théorème de Fermat, la démonstration est ainsi achevée.

















































