Entier de Dirichlet - Définition
La liste des auteurs de cet article est disponible ici.
Structures
Un entier de Dirichlet tire son intérêt de l'ensemble de ses éléments ainsi que les lois de compositions qui s'y appliquent. Le nombre √5, en tant qu'entier de Dirichlet n'est pas inversible. Dans l'ensemble des nombres réels, ou celui des nombres de la forme a + b.√5 avec a et b rationnels, il l'est. L'entier naturel 19 est un nombre premier dans l'ensemble des nombres relatifs, dans celui des entiers de Dirichlet il est divisible comme le montre le produit 19 = (4 + 3.ω)(7 - 3.ω) et ne peut être qualifié de premier. Il est en conséquence essentiel de considérer les entiers de Dirichlet comme un tout, munis de ses propriétés propres.
Définitions
La démarche est analogue à celle définissant les entiers quadratiques, elle correspond à celle des entiers de Gauss ou d'Eisenstein.
Pour mettre en évidence cette analogie, le nombre d'or 1/2.(1 + √5) est ici, et dans le reste de l'article désigné par la lettre ω, souvent utilisé dans ce type de situation. Comme le terme d'entier désigne ici parfois un entier quadratique et parfois un entier relatif, l'usage des lettres grecques est réservé, dans cet article, aux entiers de Dirichlet et les lettres latines aux entiers relatifs ou aux nombres rationnels. La lettre ε est utilisée pour décrire une unité, c'est-à-dire un élément inversible de l'anneau des entiers de Dirichlet.
-
- Un nombre réel α est dit entier de Dirichlet si et seulement si, il existe deux entiers relatifs a et b tel que α = a + b.ω.
Comme le montre la suite de l'article, l'ensemble des entiers de Dirichlet forme un anneau euclidien. Dans une telle structure les nombres premiers jouent un rôle essentiel. Pour éviter une confusion entre les nombres premiers usuels et ceux de l'anneau de Dirichlet, on utilise le terme suivant dans le reste de l'article :
-
- Un entier de Dirichlet π est dit nombre premier de Dirichlet seulement si toute décomposition de π en deux facteurs entiers de Dirichlet contient un et un seul élément inversible dans l'anneau.
La notion de nombre premier de Dirichlet correspond à celle d'élément premier ou d'élément irréductible. Une difficulté existe dans la définition précédente des nombres premiers, un entier ne se décompose pas de manière unique. Cette difficulté se trouve aussi pour les entiers relatifs. Au sens de la définition précédente, 4 possède deux décompositions en facteurs premiers, 2x2 et -2x-2. Pour cette raison, on définit dans Z, l'ensemble des entiers relatifs, un nombre premier comme un nombre vérifiant non seulement la propriété de la définition précédente mais qui est aussi strictement positif. Dans le cas général, à un nombre irréductible π correspond une classe d'équivalence, celle des éléments de la forme ε.π où ε décrit le groupe des unités, c'est-à-dire le groupe des éléments ayant un inverse dans l'anneau munis de la multiplication. La convention utilisée dans cet article est de n'appeler nombre premier qu'un unique représentant dans chacune des classes. Cette démarche est analogue à celle utilisée pour les entiers relatifs où seul l'entier strictement positif de la classe est considéré comme premier. Ici, le nombre premier considéré dans une classe est celui de la forme a + ω.b tel que a est strictement positif et b de valeur absolue minimale. Cette convention n'est pas générale.
Structure d'anneau
L'ensemble des entiers de Dirichlet muni de l'addition et de la multiplication forme un anneau, souvent noté Z[ω]. Cette notation décrit, en général, les polynômes dans lequel on a remplacé la variable X par ω. On obtient une expression de la forme anωn + an-1ωn-1 + ... + a1.ω + a0, ici n désigne un entier positif et les symboles ai des entiers relatifs. Le terme ω2 peut être remplacé par 1 + ω, le terme ω3 par 1 + 2.ω etc... On obtient in fine, une expression de la forme a + b.ω où a et b désignent deux entiers relatifs.
Cette propriété est générale aux entiers d'un corps de nombre (cf l'article Entier algébrique). Il est néanmoins simple de vérifier ici que l'ensemble est un sous-anneau du corps des nombres réels (tout corps est aussi un anneau). On remarque que :
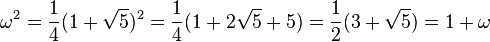
Ce qui permet d'établir la stabilité de l'ensemble pour les différentes opérations :
![\forall a_1,a_2,b_1,b_2 \in \mathbb{Z} \quad (a_1+\omega.b_1)-(a_2+\omega.b_2)=(a_1-a_2)+\omega.(b_1-b_2)\in \mathbb{Z}[\omega]](https://static.techno-science.net/illustration/Definitions/autres/4/400e8ab62331abe51b581274ff6525e6_6acce46c83d944daf45070088683b552.png)
![\forall a_1,a_2,b_1,b_2 \in \mathbb{Z} \quad (a_1+\omega.b_1).(a_2+\omega.b_2)=(a_1.a_2+b_1.b_2)+\omega.(a_1.b_2+b_1.a_2+b_1.b_2)\in \mathbb{Z}[\omega]](https://static.techno-science.net/illustration/Definitions/autres/2/225969256c65940cc9cf52074e862cda_122722aca853b58371f61da5f4c2eff5.png)
En tant que sous-anneau du corps R des nombres réels, l'anneau de Dirichlet hérite de certaines propriétés, ainsi l'anneau est intègre et commutatif. Il est de plus unitaire et de caractéristique nulle. Dire qu'un anneau est de caractéristique nulle revient à dire qu'une somme de type 1 + 1 + ... + 1 n'est jamais égale à 0. Un anneau de caractéristique nulle contient une copie de Z, l'anneau des entiers relatifs, engendré par l'élément neutre de l'addition.
Corps des fractions
Il existe une technique générale qui permet de plonger un anneau dans un corps si l'anneau est commutatif unitaire et intègre. Un corps est un anneau dont tous les éléments, à l'exception de 0 l'élément neutre de l'addition, sont inversibles. Le terme plonger signifie que chaque élément de l'anneau est considéré comme un élément du corps. Cette technique est utilisée pour construire Q, le corps des nombres rationnels. Comme pour le cas des entiers relatifs, un élément du corps des fractions de l'anneau des entiers de Dirichlet est obtenu par une fraction de deux entiers de Dirichlet telle que le dénominateur n'est pas nul. Elle est toujours de la forme a + b.√5 où a et b sont des nombres rationnels. On les appelle dans cet article des rationnels de Dirichlet.
-
- Si α est un rationnel de Dirichlet alors il existe deux rationnels a et b tel que α = a + b.√5.
En effet, soient c, d, e et f quatre entiers relatifs tel que e + f.ω soit non nul, (c'est-à-dire soit e soit f est non nul), on obtient :
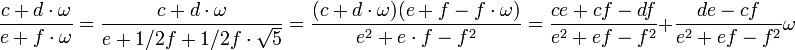
Le terme du dénominateur ne peut être nul car il est le produit de deux facteurs non nuls. Ces égalités démontrent le résultat cherché, en effet :
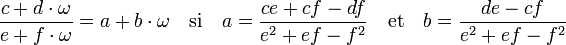
-
- Si a et b sont deux rationnels, alors a + b.√5 est un élément du corps des fractions de l'anneau des entiers de Dirichlet.
Pour s'en assurer, le plus simple est de trouver le dénominateur commun à a et à b, l'expression s'écrit alors comme une fraction de numérateur un entier de Dirichlet et de dénominateur un entier relatif, qui est aussi un entier de Dirichlet.
L'ensemble des fractions formées par les entiers de Dirichlet forme un corps. Cette propriété est une conséquence de la définition des opérations sur les fractions. On en déduit que l'ensemble des rationnels de Dirichlet forme un corps, en général noté Q[√5].

















































