Entropie de Shannon - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Voici quelques propriétés importantes de l'entropie de Shannon :
Définition formelle
Pour une source, qui est une variable aléatoire discrète, X comportant n symboles, un symbole i ayant une probabilité Pi d'apparaître, l'entropie H de la source X est définie comme :
où
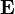
L'entropie ainsi définie vérifie les propriétés suivantes :
-
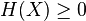
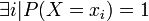
-
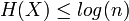
- elle est maximale pour une distribution uniforme, c’est-à-dire quand tous les états ont la même probabilité ;
- toutes choses égales par ailleurs, elle augmente avec le nombre d'états possible (ce qui traduit l'intuition que plus il y a de choix possibles, plus l'incertitude est grande) ;
- elle est continue
Justification du logarithme
L'utilisation du logarithme peut paraître arbitraire à première vue. Il faut se souvenir que l'effet du logarithme est de transformer la multiplication en addition et la division en soustraction. Par ailleurs, étant donné deux variables aléatoires indépendantes X et Y, la probabilité du produit cartésien de ces variables aléatoires est donnée par :
Ainsi:
Ce qui est intuitivement satisfaisant puisque X et Y sont indépendantes. L'entropie étant une mesure d'information moyenne contenue dans une variable aléatoire, l'entropie de la combinaison de deux variables qui ne sont pas reliées entre-elles s'additionne simplement. On voit alors le travail qu'effectue le logarithme en effectuant le pont entre la multiplication des probabilités et l'addition des entropies. Dans le cas où il existe une certaine dépendance entre X et Y, on vérifie par une preuve semblable que :
La quantité H(X,Y) est appelée l'entropie conjointe des variables X et Y.
Maximisation de l'entropie
Inégalité de Locatelli-Mabon
La proposition précédente, suivant qu'une distribution d'événements équiprobables maximise l'entropie pour un nombre donné d'éléments K, peut être exprimée plus généralement par l'inégalité de Locatelli-Mabon :
où qi est une distribution de probabilités quelconque sur la variable X. On voit alors que l'inégalité précédente est obtenue en tant que cas particulier lorsque 1 / qi = K, c'est-à-dire pour des événements équiprobables :
Démonstrations
Preuve par l'inégalité de Jensen
Le logarithme est une fonction concave, c'est-à-dire que sa dérivée seconde est inférieure ou égale à zéro pour toute valeur de x sur son domaine. Par Jensen nous obtenons alors :
Puis en posant :
En substituant dans Jensen :
Et en développant les espérances mathématiques :
Par la propriété des logarithmes :
CQFD.
Preuve par une borne linéaire sur le logarithme
Il est facile de vérifier que la fonction logarithmique est bornée supérieurement par n'importe quelle droite tangente à celle-ci. La nature concave de la fonction logarithme lui confère cette propriété :
On a ainsi :
La fin de la preuve est la même que précédemment, par la propriété des logarithmes :
CQFD.
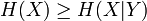
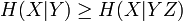
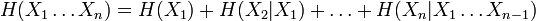
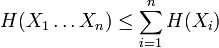
![H_b(X)= -\mathbf E [\log_b {P(X=x_i)}] = \sum_{i=1}^nP_i\log_b \left(\frac{1}{P_i}\right)=-\sum_{i=1}^nP_i\log_b P_i.\,\!](https://static.techno-science.net/illustration/Definitions/autres/c/cbd6017f6595705730de32b0f8142582_e2d662fc330c29a4e04d7cc429657121.png)
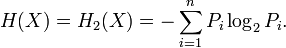
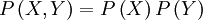
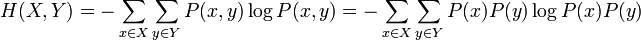
![\Rightarrow H(X,Y)=-\sum_{x \in X}\sum_{y \in Y} P(x)P(y)\left[\log P(x) + \log P(y)\right]](https://static.techno-science.net/illustration/Definitions/autres/2/2c90040a555749b86c8551f3b6dbedd1_245dbfba8d412a94a519f0466e89fa58.png)
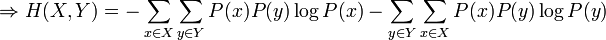
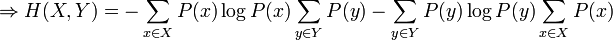
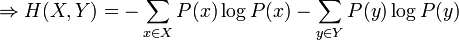
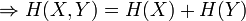
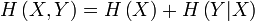
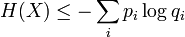
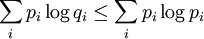
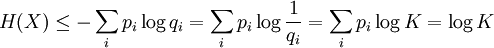
![E[f(X)] \leq f(E[X])](https://static.techno-science.net/illustration/Definitions/autres/7/785ba5bab8d7fb99157372f9181345f3_bcc446523238f0a8f353137647ed9c37.png)
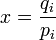
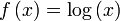
![E\left[\log \frac{q_i}{p_i}\right] \leq \log \left(E\left[\frac{q_i}{p_i}\right]\right)](https://static.techno-science.net/illustration/Definitions/autres/c/ce8002e51230f1f343b06ac2f0b60993_1df7e18a6fe0e563b03e4f38ad68b856.png)
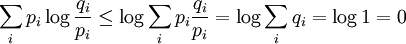
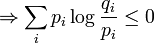
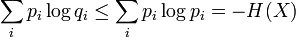
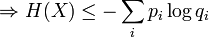
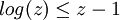
![\sum_i p_i \log \frac{q_i}{p_i} \leq \sum_i p_i \left[ \frac{q_i}{p_i} - 1 \right]=\sum_i \left[q_i - p_i \right]=\sum_i q_i - \sum_i p_i=1-1=0](https://static.techno-science.net/illustration/Definitions/autres/f/fdc377e1f3cf635f9bb5f66a52dc7083_d5711ae0d5a8d6f978843ea909f041e5.png)

















































