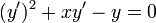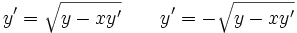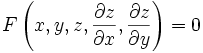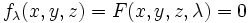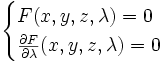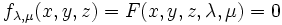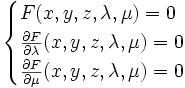Enveloppe (géométrie) - Définition

Utilisation pour les équations différentielles

Équations différentielles ordinaires

Tracé de quelques solutions de (y')^2+xy'-y=0. En bleu les solutions régulières, en vert la solution singulière, en rouge la solution hybride mentionnée dans le texte

Une équation différentielle sous forme implicite ne vérifie a priori pas le théorème d'existence et d'unicité de Cauchy-Lipschitz. Il existe des domaines sur lesquels on peut la mettre sous forme d'une ou plusieurs équations explicites, puis il convient d'effectuer des raccordements.

Ainsi pour l'équation

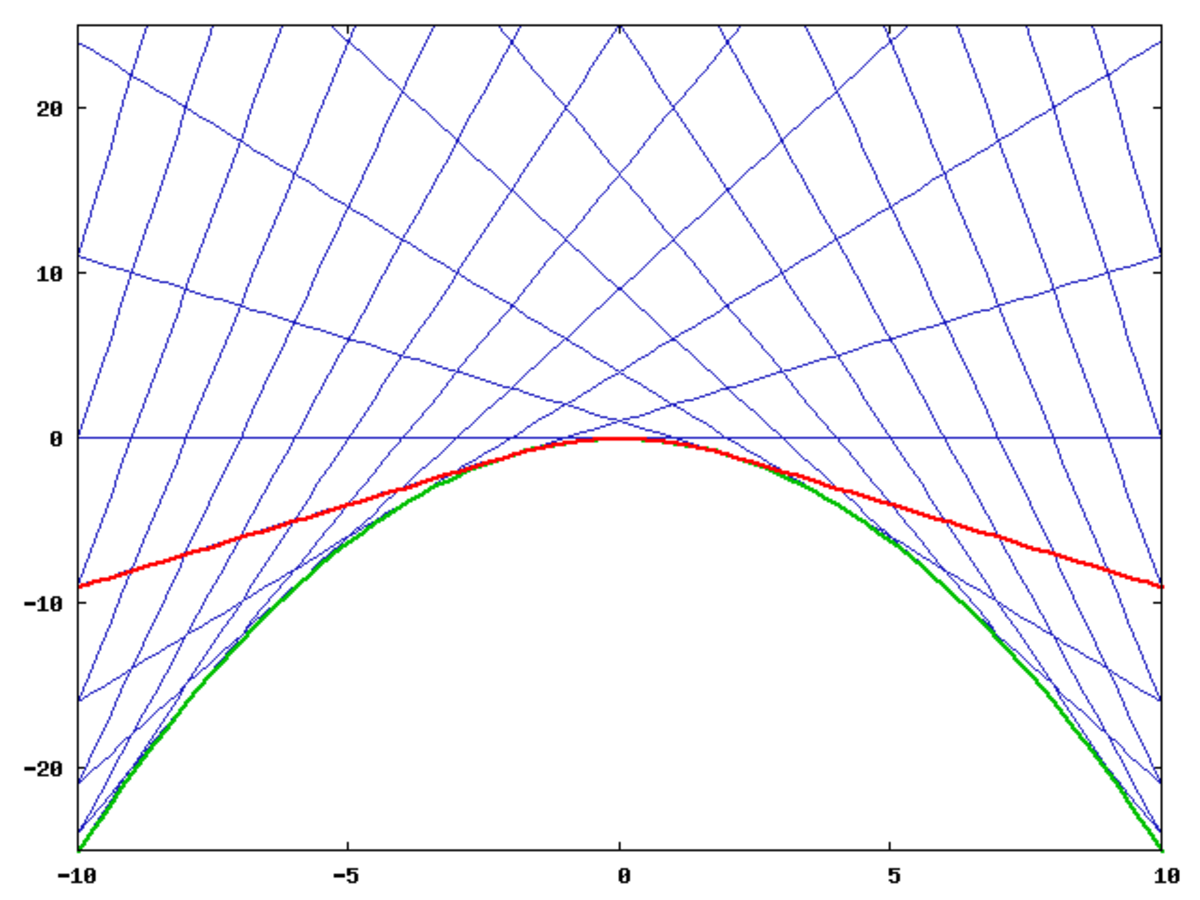
il faut distinguer trois régions : la parabole , et les deux domaines qu'elle délimite. Dans la partie supérieure, l'équation peut être mise sous l'une des deux formes résolues

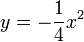
qui donne les solutions régulières tracées en bleu sur la figure ci-contre.

L'enveloppe de ces solutions est la parabole tracée en vert, qui constitue une solution, qualifiée de solution singulière. Il existe également des solutions « hybrides » formées en raccordant de façon un arc de parabole (verte) avec les solutions régulières (bleues). Un exemple de telle solution a été tracé en rouge.

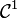
Comme pour la théorie des enveloppes, la situation est mieux décrite en se plaçant dans un espace à une dimension supplémentaire : l'espace (x,y,y').

Équations aux dérivées partielles d'ordre 1

Lorsqu'on résout une équation aux dérivées partielles d'ordre 1

on recherche des familles à deux paramètres de surfaces solutions. De telles familles sont appelées intégrales complètes de l'équation.

De même qu'avec les équations différentielles, les enveloppes (à un ou deux paramètres) de familles de solutions sont elles aussi solutions. Les enveloppes à un paramètre sont appelées intégrales générales de l'équation ; les enveloppes à deux paramètres en sont des intégrales singulières.

La notion d'intégrale complète ou générale est une notion relative. Il existe plusieurs intégrales complètes, lorsqu'on en choisit une, les autres sont obtenues comme intégrales générales.

Un lien

• Un petit texte sur les enveloppes

Enveloppe d'une famille de surfaces

Famille à un paramètre

Soit une famille de surfaces Σ_λ, indexée par un paramètre λ de façon différentiable, d'équation

L'enveloppe de cette famille de surfaces sera, si elle existe, la surface d'équations

De nouveau, l'enveloppe est tangente à toutes les surfaces de la famille. Elle intersecte chaque surface selon une courbe caractéristique qui peut être décrite également comme la courbe d'intersection de la surface avec une surface infiniment proche. Du moins ces propriétés sont elles vraies « en général », comme pour les enveloppes de familles de courbes.

Exemple : prendre une famille de sphères de même rayon centrées sur l'axe (Oz). Leur enveloppe sera un cylindre de révolution.

Famille à deux paramètres

Soit une famille de surfaces à deux paramètres Σ_λ,μ d'équation

L'enveloppe de cette famille de surfaces sera, si elle existe, la surface d'équations

L'enveloppe est tangente à toutes les surfaces de la famille. Elle intersecte chaque surface selon des points caractéristiques qui peuvent être décrits également comme les points d'intersection de la surface avec les surfaces infiniment proches (les deux paramètres variant simultanément). Du moins ces propriétés sont elles vraies « en général ».

Exemple : prendre une famille de sphères de même rayon centrées sur le plan (Oxy). Leur enveloppe sera la réunion de deux plans parallèles.