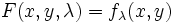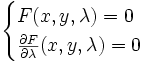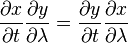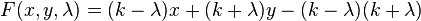Enveloppe (géométrie) - Définition

Introduction

Enveloppe (en rouge) d'une famille de paraboles passant par l'origine et dont les sommets appartiennent à une même ellipse (en bleu)

En géométrie différentielle une famille de courbes planes possède fréquemment une courbe enveloppe. Celle-ci admet deux définitions géométriques traditionnnelles, presque équivalentes :

• l'enveloppe est une courbe tangente à chacune des courbes de la famille.
• elle est le lieu des points caractéristiques, points d'intersection de deux courbes infiniment proches

De façon plus précise, l'enveloppe possède une définition analytique, c'est l'ensemble des points critiques de l'application de projection associée à la famille de courbes.

Les enveloppes rendent compte de certains phénomènes très communs, tels que les caustiques. Elles sont utiles en analyse pour décrire les solutions singulières des équations différentielles ou aux dérivées partielles, comme enveloppes de solutions régulières.

On définit de même l'enveloppe d'une famille de surfaces dans l'espace, ou plus généralement d'une famille d'hypersurfaces ou même de variétés en dimension quelconque.

Enveloppe d'une famille de courbes du plan

Introduction des équations de l'enveloppe

La caustique est l'enveloppe des rayons lumineux réfléchis par ce miroir ciculaire

On considère une famille de courbes Γ_λ, indexée par un paramètre λ. Pour chaque valeur de λ, l'équation de la courbe est supposée de la forme f_λ(x,y)=0. On suppose enfin que la famille dépend du paramètre de façon différentiable, c'est-à-dire que

est une application différentiable.

On cherche les conditions sur une courbe pour qu'au point de paramètre λ elle soit tangente à la courbe définie par f_λ. Une telle courbe est solution du système d'équations

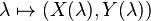
On appelle enveloppe de la famille de courbes Γ_λ la courbe vérifiant ce système d'équations. L'existence de l'enveloppe n'est pas toujours assurée. Ainsi une famille de droites parallèles ou une famille de cercles concentriques ne possèdent pas d'enveloppe. Mais si elle existe, la courbe enveloppe est « en général » tangente à toutes les courbes de la famille (le système d'équations est seulement une condition nécessaire pour cela ; la question est reprise en détails plus bas).

La famille de courbes peut aussi être donnée en représentation paramétrique, avec des équations , les fonctions en jeu étant différentiables. Dans ce cas, l'enveloppe s'obtient en résolvant l'équation

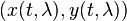
Exemples

Un calcul d'enveloppe facile à réaliser matériellement consiste à relier par des ficelles des pointes formant une figure simple. Ainsi, on peut construire deux rangées de pointes formant des intervalles réguliers, et relier successivement les pointes de l'une et l'autre rangée. L'enveloppe est la courbe « dessinée » par l'entrelacs de ficelles.

Pour simplifier, quitte à effectuer un changement de repère, on peut supposer que les pointes sont disposées le long des deux axes de coordonnées. On représente par k le décalage entre les deux séries de points qu'on relie. De ce fait

La résolution donne λ = (x − y) / 2 puis l'équation qui est celle d'une parabole. Le changement de repère effectué initialement ne modifie pas la réponse : on obtient une parabole, ou plutôt un arc de parabole puisque la figure est limitée.

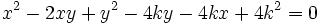
Le même mode de construction dans l'espace à trois dimensions permet d'obtenir des surfaces réglées.

Parmi les exemples les plus classiques de calculs d'enveloppes on peut citer les résultats suivants : si Γ est un arc plan birégulier

• la famille des tangentes à Γ a pour enveloppe l'arc Γ lui-même
• la famille des normales à Γ a pour enveloppe la développée de Γ, lieu des centres de courbure successifs.
• la famille des cercles de rayon a (nombre fixé) centrés sur la courbe admet pour enveloppe une courbe parallèle à l'arc Γ.

Intersection de courbes infiniment proches

Les équations définissant l'enveloppe peuvent être interprétées d'une autre façon. On prend pour référence la courbe Γ_λ, et on observe les courbes Γ_μ pour les valeurs de μ assez proches de λ. On peut étudier les points d'intersection de ces deux courbes, et passer à la limite lorsque μ tend vers λ. Les points limites obtenus sont appelés des points caractéristiques et se situent sur l'enveloppe de la famille de courbes. Ce sont les « points d'intersection de Γ_λ avec une courbe infiniment proche ».

Certains auteurs définissent la courbe enveloppe comme l'ensemble de ces points d'intersection, d'autres comme une courbe tangente à toutes les courbes de la famille. Ces deux points de vue sont équivalents à la définition par équations, sauf en un certain nombre de points exceptionnels.

Problème de projection associé

Les équations de l'enveloppe possèdent elles aussi une origine géométrique. Il faut pour en effectuer l'interprétation se placer dans l'espace à trois dimensions (x,y,λ). L'équation générale de la famille F(x,y,λ)=0 se lit alors comme l'équation d'une surface dans un espace à trois dimensions. Les courbes de la famille sont les sections « horizontales » de cette surface.

On considère les points de la surface qui sont également points critiques de l'application de projection , c'est-à-dire les points où le plan tangent à la surface est « vertical ». Les projetés de ces points critiques sont les points caractéristiques de la famille de courbes, leur réunion est l'enveloppe de la famille.

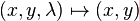
Il est possible de décrire le comportement aux points particuliers. Notamment la courbe formée par les points critiques peut avoir elle-même une tangente verticale. En un tel point, la courbe enveloppe admet un point singulier, et on perd éventuellement la propriété de tangence à la famille de courbes. Une étude plus détaillée relève de la théorie des singularités.