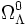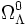Jeudi 1er Mai 2025
Rechercher 🔍

Équations de Friedmann - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Les deux équations de Friedmann - Solutions avec plusieurs espèces - Quelques solutions particulières - Interprétation - Autres écritures - Dérivation des équations de Friedmann

Solutions avec plusieurs espèces

Dans le cas où plusieurs espèces ou formes de matière emplissent l'univers et participent notablement aux équations de Friedmann, il faut tenir compte de leurs équations d'état respective et de leur abondance relative. Dans le cas de deux espèces, par exemple, la première équation de Friedmann se réécrit

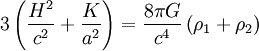
3 \left(\frac{H^2}{c^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \left(\rho_1 + \rho_2\right) .

Si l'on appelle w et w les rapports de la pression à la densité d'énergie de chacune des deux espèces et qu'on les suppose constants au court du temps, on peut réécrire cette équation à l'aide de diverses variables adimensionnées, sous la forme

\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right] ,

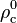
où l'on a défini, à partir d'un époque de référence notée avec l'indice ou l'exposant 0 la densité critique \rho^0_{\rm{c}} par

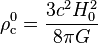
\rho^0_{\rm{c}} = \frac{3 c^2 H^2_0}{8 \pi G} ,

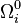
ainsi que les quantités sans dimension appelées paramètres de densité \Omega_i^0 par

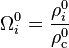
\Omega_i^0 = \frac{\rho_i^0}{\rho_{\rm{c}}^0} ,

et le facteur d'échelle normalisé, x, par x = a / a0.

En prenant une époque de référence, que l'on note avec l'indice ou l'exposant 0, on a

3 \left(\frac{H^2}{c^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \left[\rho^0_1 \left(\frac{a_0}{a}\right)^{3(1 + w_1)}+ \rho_2^0 \left(\frac{a_0}{a}\right)^{3(1 + w_2)}\right] .

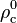
On introduit la densité critique \rho^0_{\rm{c}} par

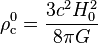
\rho^0_{\rm{c}} = \frac{3 c^2 H^2_0}{8 \pi G} ,

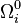
ainsi que les quantités sans dimension appelées paramètres de densité \Omega_i^0 par

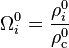
\Omega_i^0 = \frac{\rho_i^0}{\rho_{\rm{c}}^0} .

Ainsi, on obtient, en introduisant le facteur d'échelle normalisé x = a / a0,

\frac{H^2}{H_0^2} + \frac{K c^2}{H_0^2 a_0^2} \frac{1}{x^2} = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right] .

En évaluant cette quantité à l'époque de référence, il vient alors

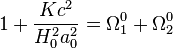
1 + \frac{K c^2}{H_0^2 a_0^2} = \Omega^0_1 + \Omega_2^0 ,

d'où finalement

\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 + \left(\Omega^0_1 + \Omega_2^0 - 1\right)\frac{1}{x^2} = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right] .
 

Cette expression se simplifie quand la densité totale égale la densité critique, ou, de façon équivalente quand la somme des paramètres de densité vaut 1. On a alors

\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right] .

Chacune de ces deux expressions se généralise à un nombre arbitraire de composantes. Des solutions exactes existent pour certaines valeurs des paramètres w et w.

En particulier, dans le cadre du modèle standard de la cosmologie, l'univers peut être décrit comme étant rempli de trois types d'espèce : de la matière relativiste (neutrinos et rayonnement), de la matière non relativiste (matière baryonique et matière noire), et de l'énergie noire, que l'on va ici approximer par une constante cosmologique. Les abondances relatives de ces espèces, qui varient avec le temps font qu'il n'arrive jamais qu'elles coexistent avec chacune des densités d'énergie significatives. À l'époque actuelle, on trouve essentiellement de l'énergie noire et de la matière non relativiste, alors qu'aux époques reculées, on trouvait de la matière relativiste et non relativiste, la constante cosmologique étant négligeable. Ceci vient du fait que les abondances de ces différents types de matière varient au cours du temps selon 1 / x3(1 + w) : la densité d'énergie associée à la constante cosmologique reste constante, alors que celle de la matière relativiste ou non relativiste croît à mesure que l'on remonte vers le passé.

Poussière et radiation

Quand on remonte vers le passé, les densités de matière non relativiste (« poussière ») ou relativiste (« radiation ») croissent comme x − 3 et x − 4 respectivement. On a donc

\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\frac{\Omega^0_{\rm{m}}}{x^3} + \frac{\Omega^0_{\rm{r}}}{x^4}\right] ,

avec

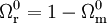
\Omega^0_{\rm{r}} = 1 - \Omega^0_{\rm{m}} .

L'intégration donne

\frac{4 \left(1 - \Omega^0_{\rm{m}}\right)^\frac{3}{2}}{3\left(\Omega^0_{\rm{m}}\right)^2} \left[1 - \sqrt{1 + \frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}}\left(1 - \frac{1}{2}\frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}\right)\right] = H_0 t .

On simplifie l'équation de départ en

\left(\frac{x {\rm{d}}x}{H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}\right] ,

soit

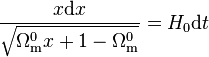
\frac{x {\rm{d}}x}{\sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}}} = H_0 {\rm{d}} t .

On effectue le changement de variable

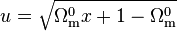
u = \sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}} ,

dont on tire

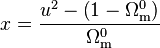
x = \frac{u^2 - \left(1 - \Omega^0_{\rm{m}}\right)}{\Omega^0_{\rm{m}}} ,
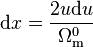
{\rm{d}} x = \frac{2 u {\rm{d}} u}{\Omega^0_{\rm{m}}} .

L'équation à résoudre devient

\frac{2 \left[u^2 - \left(1 - \Omega^0_{\rm{m}}\right)\right]{\rm{d}} u}{\left(\Omega^0_{\rm{m}}\right)^2} = H_0 {\rm{d}} t ,

qui s'intègre immédiatement en

\frac{2}{\left(\Omega^0_{\rm{m}}\right)^2} \left[\frac{u^3}{3} - \left(1 - \Omega^0_{\rm{m}}\right) u\right]^u_{u_i} = H_0 t ,

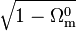
la quantité ui correspondant à la valeur x = 0, soit \sqrt{1 - \Omega^0_{\rm{m}}} . On trouve alors

\frac{2}{\left(\Omega^0_{\rm{m}}\right)^2} \left[\sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}} \left( \frac{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}}{3} - \left(1 - \Omega^0_{\rm{m}}\right)\right) + \frac{2}{3} \left(1 - \Omega^0_{\rm{m}}\right)^\frac{3}{2} \right] = H_0 t ,

soit

\frac{4 \left(1 - \Omega^0_{\rm{m}}\right)^\frac{3}{2}}{3\left(\Omega^0_{\rm{m}}\right)^2} \left[1 - \sqrt{1 + \frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}}\left(1 - \frac{1}{2}\frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}\right)\right] = H_0 t .
 

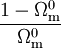
Selon la valeur de x par rapport à \frac{1 - \Omega^0_{\rm{m}}}{\Omega^0_{\rm{m}}} , qui correspond à l'époque de transition où densité de matière relativiste et non relativiste sont égales, on retrouve deux régimes précédemment étudiés. Pour les valeurs de x petites, on obtient

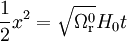
\frac{1}{2} x^2 = \sqrt{{\Omega^0_{\rm{r}}}}H_0 t ,

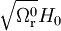
ce qui correspond au résultat pour l'univers de radiation trouvé ci-dessus, la valeur de H0 étant remplacée par \sqrt{{\Omega^0_{\rm{r}}}}H_0 , correspond à la valeur qu'aurait la constante de Hubble en l'absence de matière non relativiste.

Dans l'autre régime, on trouve

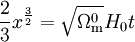
\frac{2}{3} x^\frac{3}{2} = \sqrt{{\Omega^0_{\rm{m}}}}H_0 t ,

qui là encore redonne le résultat de l'univers de poussière à la correction sur la valeur de la constante de Hubble près.

Poussière et constante cosmologique

Les seconds cas particuliers importants sont celui d'un univers dominé par de la matière non relativiste (w = 0) et dont la constante cosmologique (w = -1) devient dominante. C'est selon toute vraisemblance dans une situation similaire que se trouve notre univers, l'accélération de l'expansion de l'univers attestant de l'existence d'une forme de matière se comportant de façon assez voisine à une constante cosmologique. 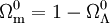Dans ce cas, l'intégration des équations de Friedmann donne, avec \Omega_{\rm{m}}^0 = 1 - \Omega_\Lambda^0 ,

\frac{a}{a_0} = \left[\sqrt{\frac{1 - \Omega_\Lambda^0}{\Omega_\Lambda^0}} \sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} H_0 t\right) \right]^\frac{2}{3} .

On reprend à nouveau la même équation avec les variables réduites. Dans un univers spatialement plat, on a

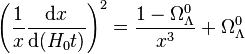
\left(\frac{1}{x}\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1 - \Omega_\Lambda^0}{x^3} + \Omega_\Lambda^0 ,

que l'on peut réécrire en

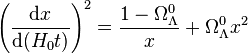
\left(\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1 - \Omega_\Lambda^0}{x} + \Omega_\Lambda^0 x^2 ,

soit

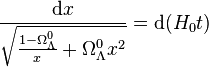
\frac{{\rm d}x}{\sqrt{\frac{1 - \Omega_\Lambda^0}{x} + \Omega_\Lambda^0 x^2}} = {\rm d}(H_0 t) ,

ou bien

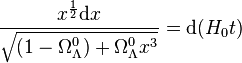
\frac{x^\frac{1}{2}{\rm d}x}{\sqrt{(1 - \Omega_\Lambda^0) + \Omega_\Lambda^0 x^3}} = {\rm d}(H_0 t) .

On pose

y = H0t,
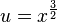
u = x^\frac{3}{2} ,

ce qui permet de réécrire l'équation précédente en

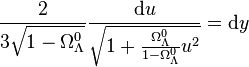
\frac{2}{3 \sqrt{1 - \Omega_\Lambda^0}}\frac{{\rm d}u}{\sqrt{1 + \frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0} u^2}} = {\rm d}y .

En posant

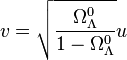
v = \sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}} u ,

d'où

\frac{2}{3 \sqrt{\Omega_\Lambda^0}}\frac{{\rm d}v}{\sqrt{1 + v^2}} = {\rm d}y .

Cette équation peut s'intégrer en

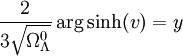
\frac{2}{3 \sqrt{\Omega_\Lambda^0}} \arg\sinh(v) = y ,

que l'on inverse en

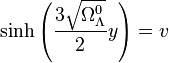
\sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} y\right) = v ,

soit

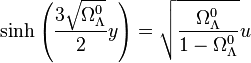
\sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} y\right) = \sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}} u ,

et finalement

\frac{a}{a_0} = \left[\sqrt{\frac{1 - \Omega_\Lambda^0}{\Omega_\Lambda^0}} \sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} H_0 t\right) \right]^\frac{2}{3} .
 

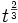
Pour les temps petits, on peut effectuer un développement limité qui redonne le comportement en t^\frac{2}{3}  :

\frac{a}{a_0} \sim \left[\frac{3}{2} \sqrt{\Omega_{\rm{m}}^0} H_0 t \right]^\frac{2}{3} .

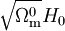
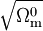
On retrouve exactement la formule déjà obtenue pour un univers de poussière, à ceci près que c'est \sqrt{\Omega_{\rm{m}}^0} H_0 qui apparaît au lieu de H0. Ceci provient du fait qu'en l'absence de constante cosmologique, la constante de Hubble serait réduite d'un facteur \sqrt{\Omega_{\rm{m}}^0} . Le fait que l'on retrouve la formule de l'univers de poussière provient du fait qu'à ces époques, la constante cosmologique est négligeable par rapport à la densité de matière.

À l'inverse, pour les temps grands, on retrouve le comportement exponentiel du facteur d'échelle par rapport au temps :

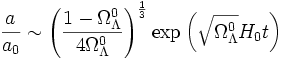
\frac{a}{a_0} \sim \left(\frac{1 - \Omega_\Lambda^0}{4 \Omega_\Lambda^0}\right)^\frac{1}{3} \exp\left(\sqrt{\Omega_\Lambda^0} H_0 t\right) .

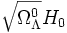
Dans ce cas, la constante de Hubble tend effectivement vers la valeur asymptotique \sqrt{\Omega_\Lambda^0} H_0 qui entre dans l'exposant. La transition entre ces deux régimes s'effectue au moment où l'argument du sinus hyperbolique est de l'ordre de 1. Quand cela se produit, la quantité a / a0 est de l'ordre de \left[\left(1 - \Omega_\Lambda^0\right) / \Omega_\Lambda^0 \right]^\frac{1}{3} . Cela correspond au moment où la densité d'énergie associée à la constante cosmologique devient de l'ordre de celle de la matière. Avant cette époque c'est celle de la matière qui domine, et l'on retrouve les résultats de l'univers de poussière, après cette époque, c'est la constante cosmologique qui domine, et l'on retrouve la dynamique de l'univers de de Sitter.

Un point intéressant est de calculer la relation entre âge de l'univers et temps de Hubble 1 / H0. On trouve ainsi

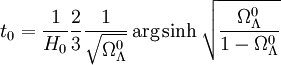
t_0 = \frac{1}{H_0}\frac{2}{3} \frac{1}{\sqrt{\Omega_\Lambda^0}} \arg\sinh\sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}} .

Pour des valeurs petites de \Omega_\Lambda^0 , on retrouve la valeur habituelle de t0 = 2 / 3H0, alors qu'à mesure que \Omega_\Lambda^0 croît (en restant bien sûr inférieur à 1), l'âge de l'univers devient plus grand que le temps de Hubble.

Les deux équations de Friedmann
Quelques solutions particulières
- Introduction - Les deux équations de Friedmann - Solutions avec plusieurs espèces - Quelques solutions particulières - Interprétation - Autres écritures - Dérivation des équations de Friedmann
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.143 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise