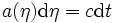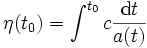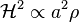Équations de Friedmann - Définition
La liste des auteurs de cet article est disponible ici.
Interprétation
Les équations de Friedmann en présence de matière non relativiste peuvent se retrouver (de façon heuristique) par un raisonnement purement newtonien. On peut en effet considérer l'évolution d'une sphère de matière, dont on suppose la densité constante à tout instant. Cette hypothèse est inexacte en général, mais la faire permet de se placer dans une situation assez semblable à celle d'un univers homogène et isotrope. auquel cas, le taux d'expansion de la sphère est relié à sa densité par la même formule que la première équation de Friedmann.
On considère donc une sphère de poussière (c'est-à-dire que l'on néglige les forces de pression) de masse M dont on étudie l'évolution du rayon R(t) en fonction du temps, sous l'effet de la gravité. Un point situé à la surface de la sphère est uniquement soumis aux forces de gravité, et obéit donc à l'équation
-
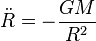
En multipliant par la dérivée de R, il vient
-
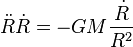
Les deux membres de l'équation correspondent à des dérivées par rapport au temps, que l'on peut intégrer en
-
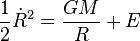
la quantité E étant alors une constante d'intégration déterminée par les conditions initiales. Cette constante d'intégration n'est rien d'autre que l'énergie totale par unité de masse, égale à la somme de l'énergie cinétique et de l'énergie potentielle :
-
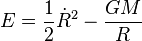
Si l'on remplace la masse de la sphère par le produit de son volume et de sa densité &\mu;, on obtient
-
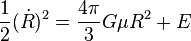
que l'on peut réécrire en
-
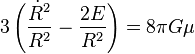
Enfin, en remplaçant la densité de masse μ par la densité d'énergie de masse ρ = μ c2, on trouve
-
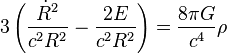
La différence cruciale entre ces deux approches vient du rôle joué par la courbure K (dans le modèle relativiste) qui s'apparente dans le modèle newtonien à une constante d'intégration sans signification géométrique. En relativité générale elle détermine les propriétés géométriques de l'espace.
Autres écritures
Dans certains cas, on peut préférer exprimer les équations en fonction du facteur d'échelle et non du paramètre de Hubble. Il vient alors
-
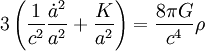
-
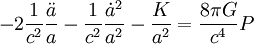
Le cas échéant, la seconde équation peut se réécrire en faisant disparaître le terme de courbure en utilisant la première, ce qui donne
-
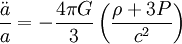
Cette dernière forme, qui donne l'accélération relative de deux objets distants du fait de l'expansion de l'univers est un cas particulier de l'équation de Raychaudhuri et pour cette raison parfois appelée ainsi. Plus généralement, toute écriture de la seconde équation de Friedmann faisant apparaître la dérivée seconde du facteur d'échelle (ou la dérivée première du taux d'expansion) peut être appelée ainsi.
Enfin, l'on peut également préférer extraire la constante cosmologique du contenu matériel de l'univers, lui donnant ainsi un rôle purement géométrique. Ce choix est aujourd'hui considéré comme peu opportun en cosmologie car la nature exacte de l'énergie noire est inconnue, mais correspond historiquement à celui d'Einstein et de Lemaître. On obtient alors, en considérant que la constante cosmologique est homogène à l'inverse du carré d'une longueur,
-
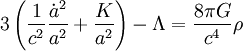
-
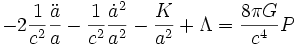
Les écritures ci-dessus utilisent le temps cosmique. Il est possible et parfois utile de lui substituer le temps conforme, η, défini par la formule
ou encore
de sorte que l'élément de longueur devienne proportionnel à une métrique de Minkowski (on dit conformément minkowskien) :
-
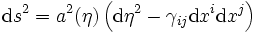
Dans ce cas, on peut définir un « paramètre de Hubble conforme »
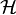
-
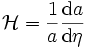
Une telle quantité n'a pas d'interprétation physique immédiate, mais permet la réécriture des équations de Friedmann en terme du temps conforme :
-
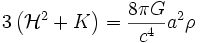
-
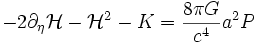
La résolution de ces équations suit sensiblement les mêmes étapes que dans les cas précédents. En particulier, on trouve les dépendances suivantes du facteur d'échelle par rapport au temps conforme :
-
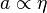
-
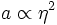
-
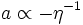
-
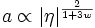
La relation
a pour conséquence immédiate que
-
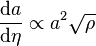
En utilisant de plus le fait que pour une équation d'état du type P = wρ, la dépendance de ρ reste
-
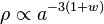
il vient
-
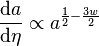
qui se résout en
-
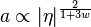
À noter que η varie de 0 à


L'intérêt de résoudre les équations de Friedmann en terme du temps conforme vient du fait que le concept d'horizon des particules et d'horizon des événements est très étroitement relié à la relation a(η), et notamment à son comportement pour les plus petites et plus grandes valeurs de η. De plus, les concepts de distance angulaire et de distance de luminosité dépendent eux aussi directement de cette même relation.