Équations de Friedmann - Définition

Introduction

Alexander Friedmann.

Les équations de Friedmann correspondent aux équations de la relativité générale (appelées équations d'Einstein) écrites dans le contexte d'un modèle cosmologique homogène et isotrope. Elles régissent donc l'évolution du taux d'expansion de l'univers et par suite de la distance entre deux astres lointains (le facteur d'échelle) et en fonction du temps appelé dans ce contexte temps cosmique. L'évolution de ces quantités est déterminée par les propriétés du contenu matériel de l'univers (rayonnement, atomes, matière noire, constante cosmologique, etc), ainsi éventuellement que la théorie de la gravitation considérée : il est en effet possible de remplacer la relativité générale par une autre théorie relativiste de la gravitation. Il peut par exemple s'agir d'une théorie tenseur-scalaire. Une autre façon de changer le modèle est de considérer la relativité générale standard mais dans un univers possédant une ou plusieurs dimensions supplémentaires. C'est le cas des modèles de cosmologie branaire.

Les équations de Friedmann tirent leur nom du physicien russe Alexandre Friedmann qui a été le premier à les écrire dans le courant des années 1920, avec un premier article traitant des espaces à courbure spatiale positive en 1922, puis un plus général en 1924 incluant le cas d'une courbure spatiale négative. Il fut suivi de près par Georges Lemaître qui retrouva ces équations en 1927, prédisant ou expliquant la loi de Hubble avant que celle-ci ne soit découverte en 1929. Auparavant, en 1917, Albert Einstein les avait écrites dans le cas particulier d'un univers statique, ainsi que Willem de Sitter dans le cas d'un univers vide de matière, mais avec une constante cosmologique. Les équations de Friedmann sous leur forme actuelle ont été retrouvées et présentées sous une forme unifiée par Howard P. Robertson en 1929, puis indépendamment par Arthur G. Walker en 1936. Pour toutes ces raisons, le type de modèle cosmologique décrit par ces équations est appelé univers de Friedmann-Lemaître-Robertson-Walker (abrégé en FLRW). Le nom de Lemaître est souvent absent, ainsi plus rarement que celui de Friedmann, ces deux personnes étant néanmoins considérées comme les vrais découvreurs de ces équations.

Les équations de Friedmann sont à la base de la quasi totalité des modèles cosmologiques, dont bien sûr le Big Bang.

Les deux équations de Friedmann

Il existe deux équations, la première reliant le taux d'expansion H, la courbure spatiale K et le facteur d'échelle a à la densité d'énergie ρ, la seconde reliant la pression P à la dérivée temporelle du taux d'expansion. La variable de temps utilisée est le temps cosmique, qui correspond essentiellement au temps mesuré sur Terre. Dans le cadre de la relativité générale, ces deux équations s'écrivent :

,

,

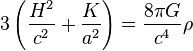
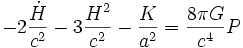
où G est la constante de Newton et c la vitesse de la lumière (la quantité 8πG / c⁴ est parfois appelée constante d'Einstein). Ces deux équations ne sont pas indépendantes : la seconde s'obtient en prenant la dérivée temporelle de la première, et en utilisant les équations de conservation, reliant la dérivée de la densité d'énergie à la pression. Quand on considère une extension de la relativité générale ou une autre théorie, ces équations sont modifiées. Pour cette raison, le terme d'équation de Friedmann est parfois employé au singulier, auquel cas la seule équation considérée est la première.

Il peut arriver (par exemple dans les modèles à dimensions supplémentaires) qu'elles ne soient plus conséquences l'une de l'autre. Dans les autres cas, il est possible de combiner les deux équations de façon à modifier la seconde, soit pour ne faire apparaître une certaine combinaison de la pression et de la densité d'énergie dans le membre de droite, soit pour ne faire apparaître que la dérivée seconde du facteur d'échelle dans le membre de gauche (voir paragraphe ci-dessous). Il est également possible d'effectuer un changement de variable pour utiliser le temps conforme plutôt que le temps cosmique. La résolution de ces équations s'effectue une fois la dépendance de la densité d'énergie et de la pression par rapport au temps ou au facteur d'échelle connus. Un certain nombre de solutions exactes sont connues.