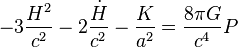Équations de Friedmann - Définition
La liste des auteurs de cet article est disponible ici.
Dérivation des équations de Friedmann
Les équations de Friedmann ne sont rien d'autre que l'écriture des équations d'Einstein décrivant un univers homogène et isotrope. Leur dérivation ne pose pas de difficulté particulière, et elles représentent même une des solutions analytiques exactes les plus simples parmi celles connues à ces équations.
L'hypothèse de l'homogénéité et de l'isotropie des sections spatiales de l'univers permet d'écrire l'élément de longueur sous la forme
- ds2 = c2dt2 − a2(t)γijdxidxj,
où γ représente la métrique des sections spatiales, décrites par les coordonnées xi. Un tel système de coordonnées est appelé coordonnées comobiles. Un observateur décrivant la trajectoire xi = Constante suit une géodésique. Il est appelé observateur fondamental. Son temps propre correspond ici exactement à la coordonnée t, appelée temps cosmique (le temps propre des observateurs fondamentaux). Une telle trajectoire correspond en première approximation aux trajectoires des galaxies, si l'on fait abstraction de leur mouvement propre. La distance entre deux observateurs fondamentaux augmente proportionnellement à la fonction a(t), qui est le facteur d'échelle. Une fois cette forme de la métrique supposée, les équations d'Einstein déterminent l'évolution temporelle du facteur d'échelle.
Les coefficients de la métrique s'écrivent
- g00 = c2,
- g0i = 0,
- gij = − a2(t)γij.
La forme exacte de γij importe peu et dépend du type de coordonnées choisi (cartésiennes ou sphériques, par exemple, si on suppose les sections spatiales euclidiennes). Le seul résultat important est de savoir que les sections spatiales étant homogènes et isotropes forment un espace à symétrie maximale, et qu'un tel espace dont la métrique serait γij a un tenseur de Ricci donné par
- 3Rij = 2Kγij,
la quantité K étant la courbure spatiale associée.
L'inverse de la métrique a pour coordonnées :
-
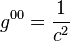
- g0i = 0,
-
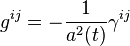
où γij représente la métrique inverse de γij.
Les symboles de Christoffel s'écrivent :
-
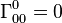
-
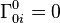
-
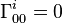
-
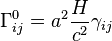
-
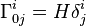
-
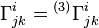
où H est le paramètre de Hubble, donne par H = da / adt, et
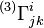
Les coefficients du tenseur de Ricci s'écrivent alors
-
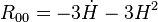
- R0i = 0,
-
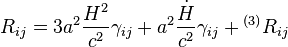
La courbure scalaire s'écrit
-
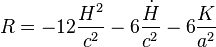
Le tenseur d'Einstein s'écrit enfin
-
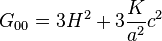
- G0i = 0,
-
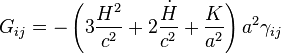
Il faut maintenant déterminer le tenseur énergie-impulsion de la matière. Le seul tenseur énergie-impulsion compatible avec les hypothèses d'homogénéité et d'isotropie utilisées est celui d'un fluide parfait. Il est alors uniquement décrit par la densité d'énergie, la pression et la quadrivitesse du fluide selon la formule
- Tμν = (P + ρ)uμuν − Pgμν.
Cette quadrivitesse correspond à celle des observateurs fondamentaux. La formule donnant la quadrivitesse étant
-
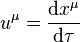
et le temps propre étant donné par le temps coordonné, on a immédiatement
- u0 = 1,
- ui = 0,
et les composantes contravariantes s'écrivent
- u0 = c2,
- ui = 0.
Les composantes du tenseur énergie-impulsion sont donc
- T00 = ρc2,
- T0i = 0,
- Tij = Pa2γij.
En utilisant la formule des équations d'Einstein, la composante 00 donne donc
-
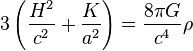
et la composante ij donne
-