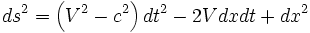Espace compact en relativité - Définition
La liste des auteurs de cet article est disponible ici.
Analogie avec l'effet Sagnac
Comme nous l'avons signalé, les raisonnements précédents sont simplistes. Nous savons qu'en relativité restreinte, on ne peut pas raisonner séparément sur l'espace et sur le temps. Les phénomènes liés à la synchronisation des horloges devraient vous être familiers et vous inciter à la prudence.
Dans ce qui précède, nous avons analysé l'espace compact comme s'il s'agissait d'une entité propre, une scène de théâtre. Nous avons fait des raisonnements purement spatiaux (comme lors de la construction des anneaux avec les règles étalons) et considéré le temps comme accessoire et venant en sus. Nous savons que cette manière de raisonner est risquée et source de problèmes.
En outre, il y a une forte analogie entre les espaces compacts et les repères en rotation (le disque en rotation).
Les deux principales analogies étant :
- La possibilité de faire un tour complet.
- L'asymétrie apparente de la vitesse de la lumière pour certains observateurs (ceux en rotation dans l'effet Sagnac).
On peut aussi ajouter que les raisonnements simplistes conduisent, comme dans l'effet Sagnac, à croire que les transformations des coordonnées appropriées sont celles de Galilée.
On peut donc considérer qu'une ligne fermée (une trajectoire un tour) dans un espace compact est analogue à la circonférence dans l'effet Sagnac. On doit donc retrouver tout ce qui existe dans l'effet Sagnac en déroulant l'espace-temps cylindrique sur le plan (comme nous l'avions déjà fait).
Nous nous limitons à une dimension spatiale par facilité (par comparaison avec la circonférence du cercle), mais cela est assez facile à généraliser à un nombre quelconque de dimensions.
L'espace-temps prend donc la forme que nous avions déjà vue :
Pour un observateur quelconque (B dans la réflexion précédente sur l'asymétrie de la vitesse de la lumière) où nous avons également représenté les trajectoires de deux rayons lumineux partant chacun dans un sens.
Ici, bien sûr, la largeur de la figure n'est plus 2π (360 degrés, un tour complet du cercle) mais la largeur de l'univers (dans ce repère).
L'inclinaison des axes de coordonnées spatiaux dépend de l'observateur (de sa vitesse, tout comme dans l'effet Sagnac).
Donc, pour tous les observateurs, l'espace est plat et l'espace-temps est de Minkowski (le fait de choisir des axes inclinés ne change rien).
c est invariant (localement) et les transformations de Lorentz sont valables.
Mais le fait que l'univers soit fermé et les axes inclinés n'est pas innocent ! N'oublions pas que l'univers se referme sur lui-même.
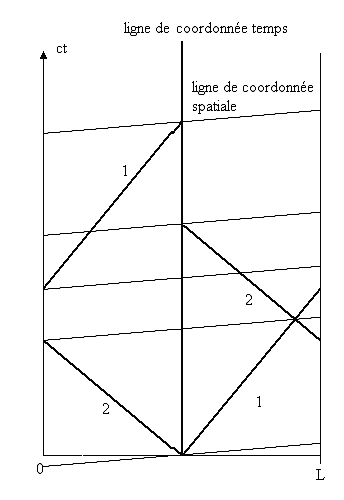
Dans le cas du cercle, cela donnait à l'espace une structure hélicoïdale. Ici, l'espace a une structure striée avec des plans spatiaux inclinés.
Dans cette figure nous avons représenté un espace à deux dimensions pour plus de clarté. Donc ici aussi on a un Time Gap. Il ne faut pas oublier qu'une trajectoire spatiale arrivant à droite repart à gauche (tour d'univers) !
Cela signifie que bien que les transformations de Lorentz soient correctes, il faut faire attention avec des trajectoires qui feraient un tour d'univers.
Ce résultat aussi montre pourquoi les raisonnements simplistes précédents ont aboutit à une conclusion erronée : l'espace-temps est différent dans les divers repères.
Il y a quand même un observateur (et un repère) privilégié. Tout comme dans l'effet Sagnac. Ici c'est celui qui observe une vitesse de la lumière globalement isotrope, pas de Time Gap et des axes spatiaux non inclinés et un espace de Minkowski classique, non strié (si ce n'est qu'il est fermé, bien sûr).
L'existence de ce repère privilégié, sans cause physique apparente, semble violer le principe de relativité. Nous en reparlerons plus loin.
Pour les observateurs en mouvement, l'espace est localement euclidien (et l'espace-temps de Minkowski) mais globalement non il a une curieuse structure striée : une ligne spatiale ne boucle jamais sur elle-même. On retrouve toutes les difficultés et subtilités de l'effet Sagnac.
La métrique décrivant la géométrie des espaces compacts relativistes est donnée ci-dessous et montre ainsi que les espaces compacts plats sont totalement compatibles avec la relativité restreinte et l'invariance de la vitesse de la lumière dans le vide contrairement à ce que semblait laisser penser l'analyse trop simple de la section précédente.
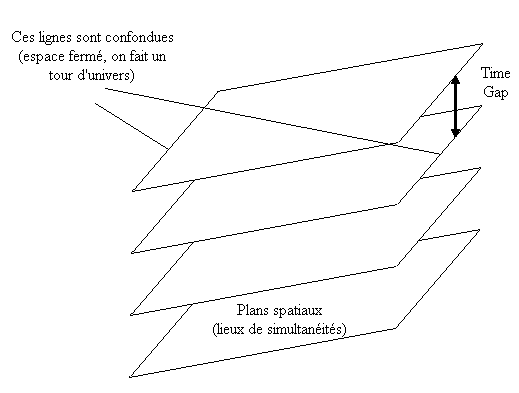
En regardant la métrique obtenue dans l'effet Sagnac, on trouve immédiatement la métrique de l'espace compact. Il faut simplement effectuer les substitutions suivantes :
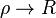
On trouve :