Espace compact en relativité - Définition

Introduction

En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac-Man : chaque plan dans lequel se déplace Pac-Man est « fermé », c'est-à-dire que Pac-Man, peu importe les déplacements qu'il fait, ne peut quitter ce plan. Il est en quelque sorte « prisonnier » de son environnement.

En physique au XXI^e siècle, les spécialistes se demandent si l'univers est une espace fermé. Malgré différents avancées théoriques et pratiques, ils ne savent avec certitude que deux choses :

• La relativité générale permet de calculer la géométrie de l'univers à partir de son contenu. Cela permet de calculer la "forme" de l'univers. C'est une partie du domaine de la cosmologie.
  Mais même comme cela il reste un peu de liberté. Une même géométrie pouvant conduire à plusieurs topologies (plusieurs formes). Nous ne savons pas comment trancher entre les différentes possibilités.
• Même si l'univers a une telle topologie compacte, sa "dimension caractéristique" (la distance pour faire un tour) doit être très grande, pratiquement au moins aussi grande que l'univers observable. Sinon cela se verrait par une analyse statistique du fond de rayonnement cosmologique fossile.

Mais même si l'univers n'a pas cette topologie étrange, il est intéressant de voir comment se comporte la relativité restreinte dans de tels espaces.

Présentation

Trajectoires dans un espace compact plat

Un espace compact est un espace fermé statique :

• Fermé : s'il est fini et sans bord.
• Statique : si sa géométrie, et en particulier ses dimensions caractéristiques, ne changent pas au cours du temps.
• Plat : si sa géométrie est analogue à la géométrie d'Euclide ou de Minkowski. C’est-à-dire en l'absence de courbure comme en relativité générale.

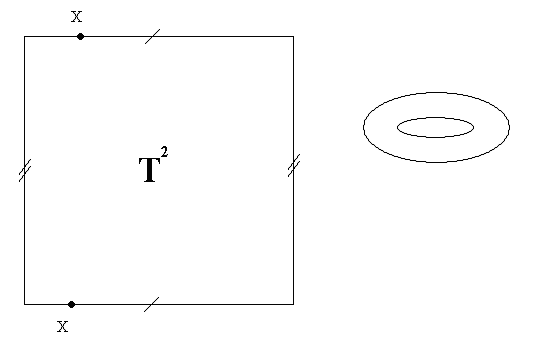
Dans l'illustration ci-dessus, les bords sont confondus. Ainsi les deux points X sont en fait identiques. Ce type d'espace est utilisé dans certains jeux vidéos où les objets qui disparaissent d'un côté de l'écran réapparaissent de l'autre. Ces bords n'ont aucune existence physique, ils sont arbitraires et peuvent être disposés comme on veut (nous y reviendrons).

Une représentation sous forme de pneu (à droite dans l'illustration) montre bien l'absence de bords. Mais un pneu est un espace à deux dimensions plongé dans l'espace ordinaire et qui possède une courbure extrinsèque (mais pas de courbure intrinsèque, qui impose la géométrie de l'espace) imposée par le repliement de la surface du pneu dans l'espace ordinaire. Nous garderons donc la représentation sous forme d'un carré qui permet de représenter le "Tore plat".

Un espace fermé n'est pas si difficile à imaginer. Il suffit de comparer à la surface de la Terre. Évidemment, pour un espace à trois dimensions c'est plus difficile à se représenter (la surface de la terre est à deux dimensions) mais la situation est tout à fait semblable. De plus, par facilité nous n'envisagerons que des espaces à deux dimensions.

Le Tore T² est un espace plat, compact. Il existe 18 variétés topologiquements différentes de ce type à trois dimensions, mais le tore suffira à illustrer notre propos, les différents raisonnements dans la suite ne dépendent pas du détail de la topologie mais seulement du fait qu'elle est fermée. De même, les raisonnements restent valables dans un espace de dimension supérieure (T³, T⁴,...).

Précisions la terminologie employée ici :

• Chemin : chemin physique. C'est le chemin emprunté par un objet. Il est unique et indépendant de l'observateur. C'est donc une suite d'événements physiques, par exemple les différentes positions d'un objet au cours du temps.
• Trajectoire : chemin vu dans un repère donné.

Il va de soit que parler d'un chemin physique est intéressant seulement en termes de référence puisque toute description doit se faire à l'aide d'un observateur, si ce n'est pour spécifier que l'on parle d'un objet déterminé dans une situation déterminée. Il convient donc de toujours bien spécifier dans quel repère on effectue l'observation. Lorsque nous parlerons de repère attaché à la feuille de papier il s'agit d'un repère dans lequel un point dans l'illustration est considéré immobile. En général, dans les figures qui suivent, le repère considéré (et indiqué) est aussi celui de la feuille de papier.

A un même chemin correspondent des trajectoires différentes selon le repère employé. Dans le cas qui nous préoccupe, nous identifierons les trajectoires avec les géodésiques. C’est-à-dire avec les chemins les plus courts entre deux points qui, dans un espace plat, sont des droites. Elles correspondent aux chemins suivis par des objets auquel aucune force s'applique (c'est le second postulat de Newton, un corps libre de forces a une vitesse constante, mais ce n'est pas capital dans la suite car ce qui nous importe ce sont les trajectoires et non les raisons pour lesquelles un corps suit celles-ci).

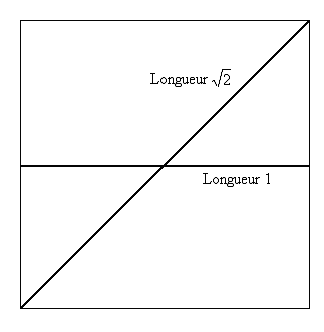
Tout espace plat compact est forcément anisotrope. C'est vrai aussi des autres variétés que nous avons suggérées. Par contre, dans un espace compact sphérique, par exemple, l'espace peut être isotrope.

Voici quelques illustrations importantes :

Géodésique :

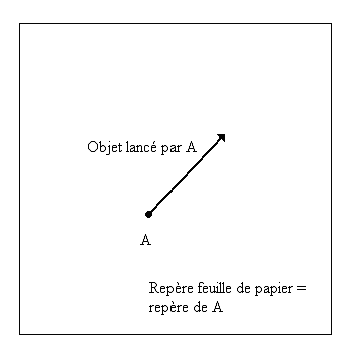
Géodésiques "un tour" :

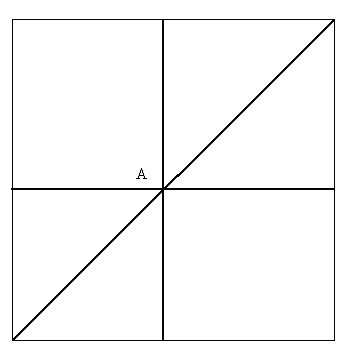
Géodésiques "deux tours" :

Selon l'angle fait par la trajectoire, l'objet peut faire plusieurs tours avant de revenir au point de départ.

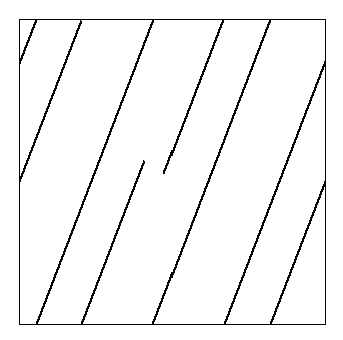
Lorsque la pente de la trajectoire est irrationnelle (si elle ne peut pas être écrite comme une fraction), l'objet fait même un nombre infini de tour avant de revenir au même point. Plus précisément il repasse une infinité de fois arbitrairement près de son point de départ mais sans jamais y repasser exactement.

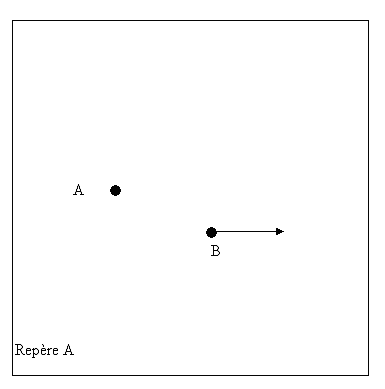
L'observateur se déplace horizontalement à la vitesse V.

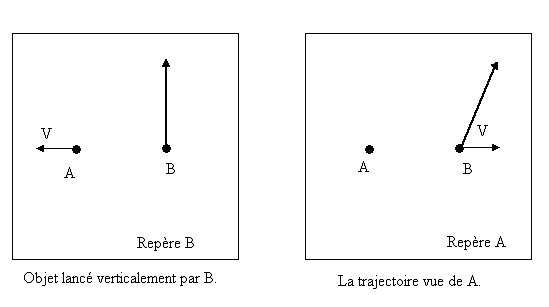
Pour le même chemin, la trajectoire dépend du repère considéré.

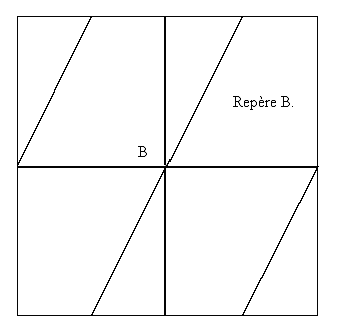
L'ensemble des trajectoires et leur comportement (1 tour, 2 tours...) est semblable pour A et pour B. Mais deux trajectoires semblables ne correspondent pas nécessairement au même chemin tout comme dans l'illustration un seul chemin a différentes trajectoires dans différents repères.

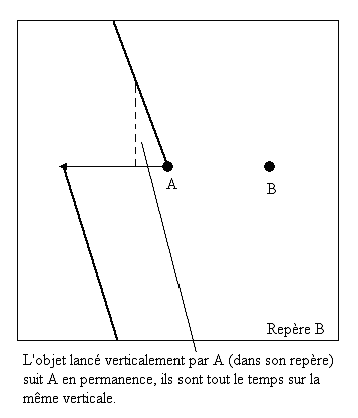
Pour A, la trajectoire est verticale et fait un tour. Pour B c'est une trajectoire à N tours (une partie seulement de cette trajectoire est représentée).

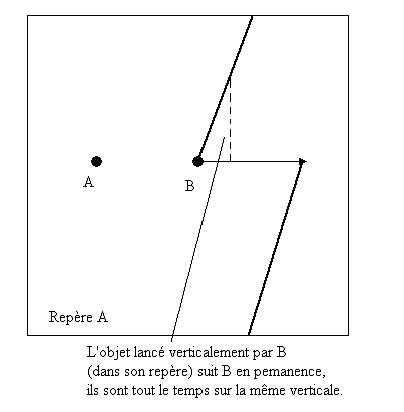
Les comportements des trajectoires sont donc strictement symétriques.

Détermination d'une vitesse absolue

Essayons de déterminer un repère absolu en vérifiant s'il est possible de déterminer l'immobilité absolue.

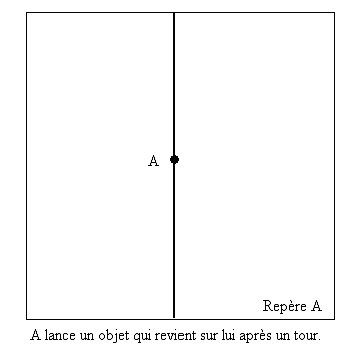
Puisque l'objet revient au même endroit après un tour et puisqu'il le rencontre en cet endroit, A en déduit qu'il est absolument immobile.

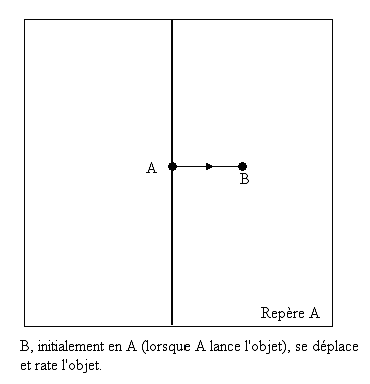
A peut donc dire que B est en mouvement absolu puisqu'un objet lancé revient au même endroit et B le "rate".

Cet argument a souvent été utilisé par des amateurs pour affirmer qu'un repère absolu existe dans les espaces compacts.

Mais quoi d'étonnant ! Nous avons entièrement raisonné dans le repère de A. Pas étonnant qu'on puisse définir une vitesse "absolument relative" (sic) à A ! Le raisonnement ci-dessus peut d'ailleurs se faire dans l'espace ordinaire, il suffit de parler de "à la verticale de" au lieu de "faire le tour". Or quoi d'étonnant que l'objet lancé par A reste à sa verticale ? C'est lui qui l'a lancé ! Pour un autre observateur l'objet, même en mouvement latéral, reste aussi à la verticale de A (nous en avons vu un exemple plus haut).

Voyons si en raisonnant dans le point de vue de B on aboutit à la même conclusion.

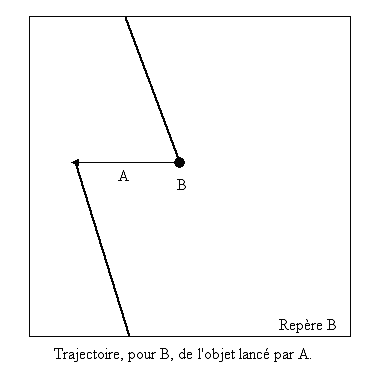
Pour B, ce chemin n'est pas une trajectoire 1 tour, comme nous l'avons vu ci-dessus.

Voyons maintenant le raisonnement de B lorsqu'il lance un objet verticalement.

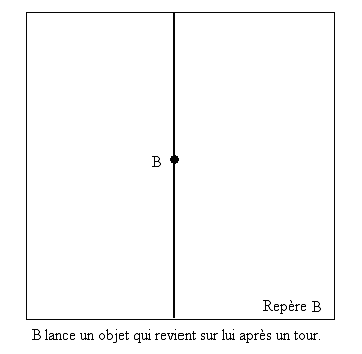
Puisque l'objet revient au même endroit après un tour et puisqu'il le rencontre en cet endroit, B en déduit qu'il est absolument immobile.

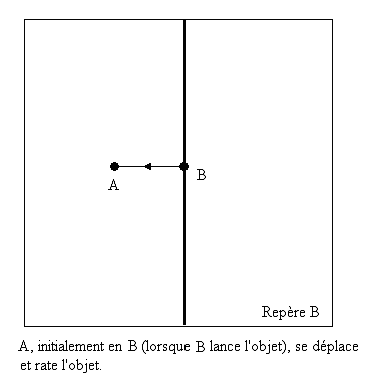
B peut donc dire que A est en mouvement absolu puisqu'un objet lancé revient au même endroit et A le "rate".

Pour A, ce chemin n'est pas une trajectoire 1 tour. Et c'est une trajectoire exactement semblable à celle vue dans le repère B plus haut (vue dans un miroir). Par exemple ce pourrait toutes les deux être des trajectoires à 23 tours.

La situation est totalement symétrique. Selon les trajectoires choisies, c'est A qui détermine un mouvement absolu de B ou l'inverse. Et la symétrie des différentes trajectoires ne permet pas de décider si c'est A ou B qui a raison.

A et B sont donc en mouvement relatif mais rien ne permet de décider du mouvement absolu et ce bien que l'espace soit anisotrope. Il peut être amusant d'étudier l'anisotropie (directions des trajectoires un tour) en fonction des observateurs (on constate que la direction des axes principaux varie).

Ce n'est que si on effectue un raisonnement incomplet que l'on croit pouvoir déterminer un repère absolu dans un espace compact. En s'arrêtant à l'illustration montrant que B se décale par rapport à une trajectoire un tour d'un objet lancé par A. Mais si l'on considère le point de vue des différents repères et l'ensemble des trajectoires possibles, on constate la parfaite symétrie entre A et B et l'absence de repère absolu. Tout comme le caractère "N tours" des trajectoires qui n'est pas absolu. C'est probablement ce qui est le plus contre intuitif, induit le profane en erreur et le conduit à tronquer son raisonnement. Il semble intuitif qu'une trajectoire "un tour" l'est dans tous les repères (elle revient au "même endroit"). Mais c'est faux car la notion de "même endroit" est elle-même relative.

Il n'y a pas de sens de parler de "revenir au même endroit" ou "au même point". Car ce point est fonction du repère c’est-à-dire de la représentation mathématique utilisée pour déterminer la position de chaque objet (ses coordonnées). On ne peut parler que de relations entre objets : de la distance entre les objets et entre objets et observateurs. Revenir au même endroit doit en fait se comprendre comme "revenir sur le même observateur". Et cette fois, comme l'observateur peut lui-même être en mouvement relativement à un autre observateur, toute référence absolue disparaît automatiquement.

En fait, suivant notre terminologie, on aurait plutôt dû parler de repère privilégié, le privilège étant donné la par la topologie de l'espace. Un tel repère n'existe pas (il existe toutefois ici des directions privilégiées) lorsque l'on parle des trajectoires.

Dans un espace courbe (par exemple sphérique) la situation est différente. La courbure imposée par exemple par la présence de matière (en relativité générale) implique la possibilité d'avoir un repère privilégié pour la vitesse.

Asymétrie de la vitesse de la lumière

Considérons l'expérience suivante :

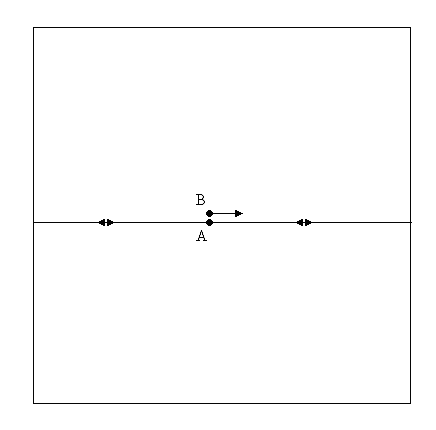
A, considéré comme immobile (nous sommes dans son référentiel), envoie deux impulsions lumineuses de chaque côté. Chaque impulsion se propage à la vitesse c. Après avoir fait le tour de l'univers, chaque impulsion revient sur A en même temps puisqu'elles se déplacent à la même vitesse.

L'observateur B est en mouvement par rapport à A. Il est au même endroit que A lorsque les deux impulsions lumineuses s'éloignent et s'est déplacé lorsque les deux impulsions reviennent.

Voyons son point de vue :

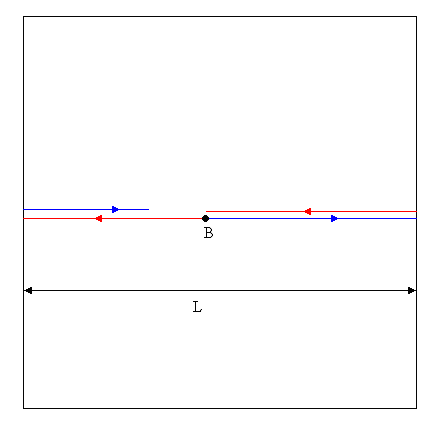
Nous sommes dans le référentiel de B. B est immobile. Les deux impulsions lumineuses (la rouge et la bleue) ne reviennent pas en même temps sur lui comme le montre cette illustration.

Dans le référentiel de B, l'univers a une longueur L.

Nous appellerons l'impulsion lumineuse bleue "1". Et toutes les variables le concernant seront indicées par 1. De même, l'impulsion lumineuse rouge sera la 2. Ainsi, l'impulsion 1 (bleue) se déplace à la vitesse c₁ (peut-être identique à c) et met le temps t₁ pour faire le tour (pour partir de B et revenir en B, pas pour arriver à l'endroit où il croise l'autre impulsion). De même pour l'impulsion 2 on a c₂ et t₂.

Tout ce que nous savons c'est qu'en général :

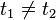
Le temps pour faire le tour est simplement donné par :

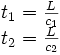
Donc :

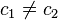
La vitesse est différente selon que le signal lumineux se propage à gauche ou à droite !

Il semble que le repère A soit très particulier puisque la vitesse de la lumière est symétrique mais pas dans B. Toutefois, on peut effectuer le même raisonnement dans B. Envoyer un signal de vitesse précise de chaque côté et en déduire que dans A les vitesses sont asymétriques.

A nouveau, si on effectue un raisonnement partiel, il semble qu'il y ait un référentiel absolu. Mais ce n'est pas le cas.

Ce qui nous importe ici, c'est qu'une asymétrie dans la vitesse de la lumière peut être constatée dans certains repères en translation uniforme. Même si l'on effectue des expériences localement, sans faire le tour de l'univers avec un signal, on doit être confronté à cette asymétrie. Or nous savons déjà qu'une telle asymétrie n'est pas constatée expérimentalement.

Il semble donc qu'un espace compact ne soit pas compatible avec l'expérience.

Mais vous aurez certainement constaté l'analogie avec la situation analogue dans l'effet Sagnac. Les raisonnements qui suivent sont équivalent à l'approche simpliste qui a été utilisée dans cet article. Nous verrons plus loin que les conclusions ne sont pas si simples. Ce qui suit est donc à prendre avec des pincettes et est donné pour bien illustrer la problématique.

Longueur de l'univers

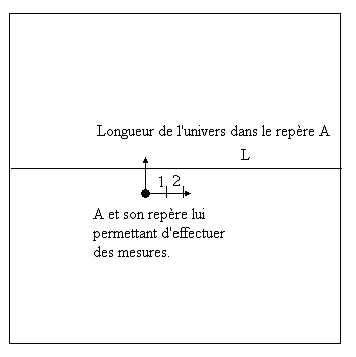
A, avec son repère, peut sans aucune difficulté mesurer la longueur d'une trajectoire "un tour" et donc mesurer la longueur de l'univers.

Que voit réellement A lorsqu'il observe une trajectoire quelconque ?

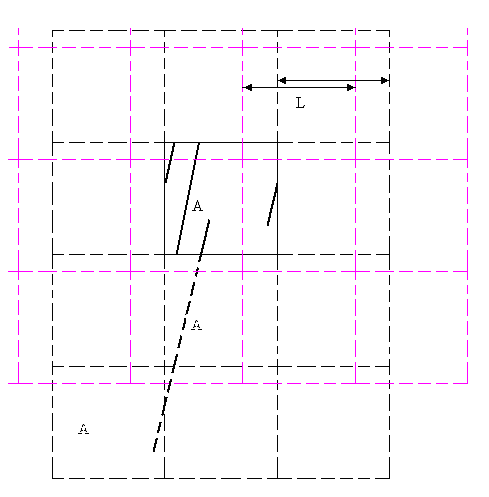
On peut prolonger le carré fictivement : une trajectoire vue de A devient rectiligne et A voit sa propre image répétée à l'infini (ainsi que la trajectoire de l'objet).

Voilà qui illustre bien que les bords sont fictifs et peuvent être placés où on veut (par exemple le quadrillage noir ou le bleu).

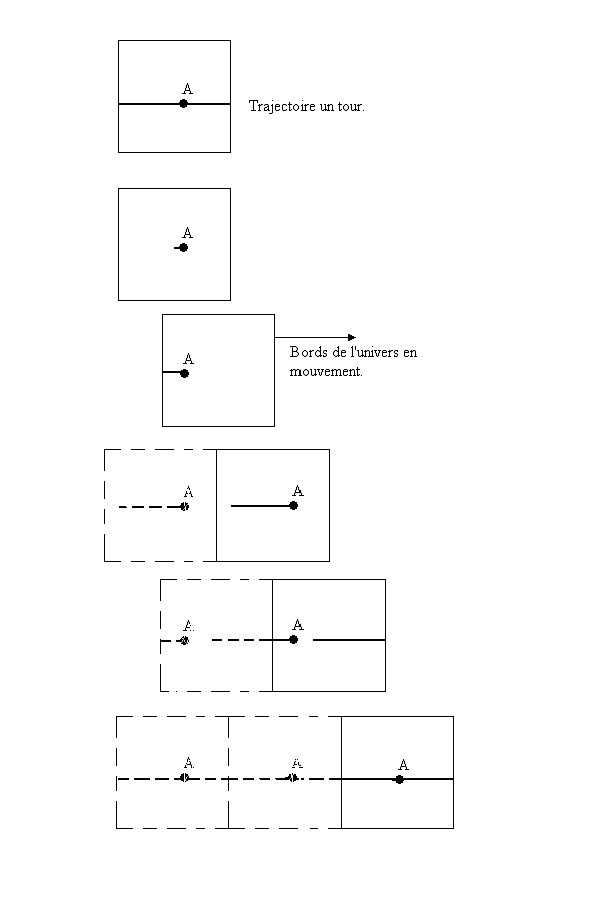
On peut même avoir des bords en mouvement. Etant fictifs et l'univers identique pour toute position des bords, l'univers est toujours le même. Evidemment une telle représentation n'est guère pratique sur papier ! Le chemin est identique, seule la trajectoire représentée sur papier varie (au cours du temps !), mais pour A il s'agit bel et bien de la même trajectoire car l'espace "prolongé" est identique (le plan complet avec l'image de A répétée à l'infini).

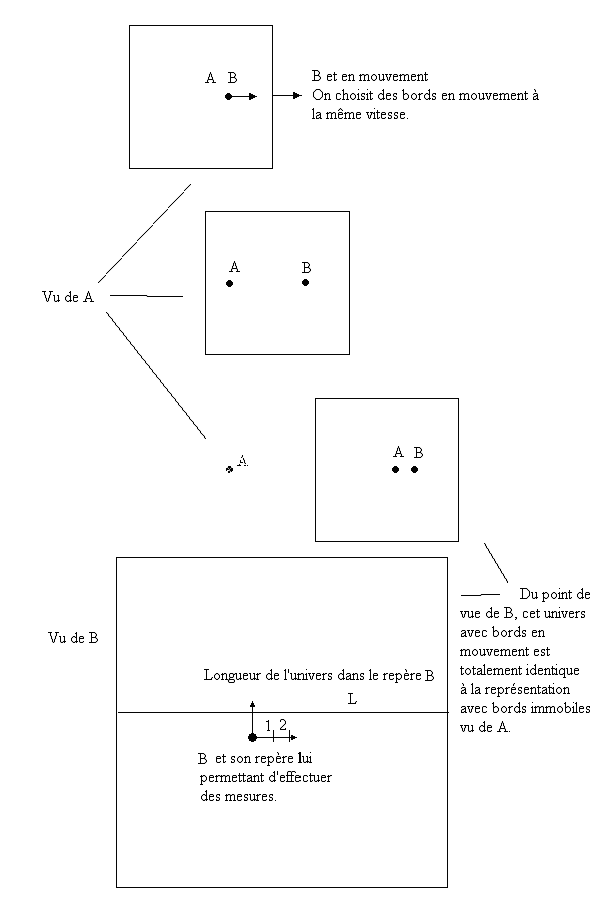
Lorsque les bords sont en mouvement avec B, à la vitesse V, la situation est strictement identique à celle de A. Cela est en accord avec ce que nous avons vu plus haut : il n'y a pas de vitesse absolue. La représentation est strictement identique à l'illustration montrant le repère de A et la longueur d'univers et l'univers est inchangé par le mouvement (fictif) des bords donc la longueur est toujours la même.

Mesures de la longueur de l'univers

Les observateurs A et B décident de mesurer la longueur de l'univers en utilisant des barres métalliques rigides identiques, des étalons de longueur.

Ils vont disposer ces barres l'une après l'autre jusqu'à faire le tour de l'univers. On obtient ainsi un gigantesque anneau de barres métalliques.

Attention : on emploie le mot anneau car il est refermé sur lui-même mais il n'est pas courbe : les segments sont en ligne droite.

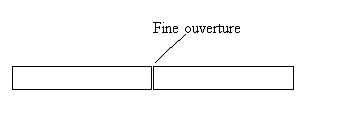
Les anneaux, sont construits en posant les barres les unes à la suite des autres mais ces barres ne sont pas soudées. Cela ne pose aucun problème puisque chacun construit son anneau dans son propre repère et les barres sont immobiles dans ce repère.

A peut donc disposer ses barres et construire son anneau.

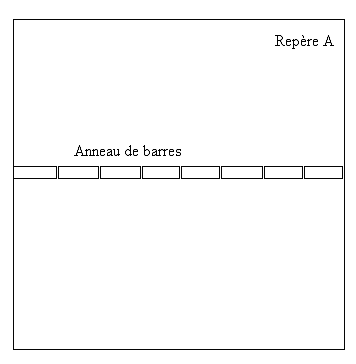
Il lui suffit de compter le nombre de barres pour connaître la longueur de l'univers.

Inutile de répéter l'illustration, B fait de même dans son repère.

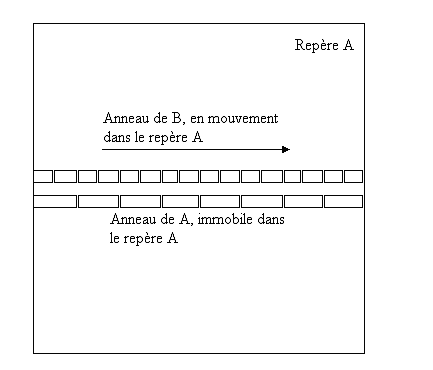
B étant en mouvement par rapport à A, les segments de B perçus par A sont plus courts (contraction des longueurs). Mais cet anneau fait aussi le tour de l'univers. A peut les comparer à un instant donné (comme s'il prenait une photo, voir l'illustration ci-dessus). Donc pour A, l'anneau de B a plus de barres.

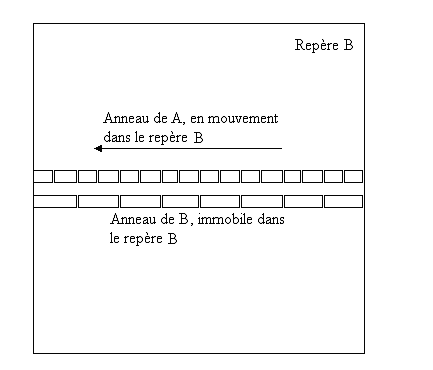
A étant en mouvement par rapport à B, les segments de A perçus par B sont plus courts (contraction des longueurs). Mais cet anneau fait aussi le tour de l'univers. B peut les comparer à un instant donné (comme s'il prenait une photo, voir l'illustration ci-dessus). Donc pour B, l'anneau de A a plus de barres.

Mais nous avons là une contradiction ! L'anneau de A ne peut pas avoir à la fois moins et plus de barres que l'anneau de B !

On ne peut invoquer des effets mécaniques qui forceraient les segments à "s'étirer", contrant la contraction des longueurs, et éliminant la contradiction, car :

• Il n'y a pas d'accélération, qui pourrait provoquer de tels effets. A et B utilisent seulement des segments construits de manière identique, immobiles dans leur repère, et les anneaux ne sont pas mis en mouvement.
• Il ne peut y avoir de "traction" sur les segments à cause du fait qu'ils font le tour de l'univers puisque les segments sont non soudés et simplement posés les uns à côté des autres.

La contraction des longueurs est une conséquence immédiate de l'invariance de c.

Donc, l'invariance de c est incompatible avec l'existence d'un espace compact.

Il ne peut y avoir contraction des longueurs dans un univers compact et donc le nombre de segments est identique pour A et B. La longueur de l'univers est la même pour les deux observateurs. En vertu de ce que nous savons déjà (repères équivalents du point de vue de l'ensemble des trajectoires, repères équivalents du point de vue de l'asymétrie des vitesses), nous pouvons donc affirmer que les repères A et B sont totalement équivalents, à tout point de vue.

Pour information

L'aspect plat de l'univers (le fait que les trajectoires soient des lignes droites), ainsi que son aspect statique, sont cruciaux pour les raisonnements effectués ci-dessus.

Donc si l'univers n'est pas plat (comme en relativité générale) ou s'il est non statique la consistance peut éventuellement être assurée. C'est le cas des métriques de Robertson Walker en relativité générale (une des solutions des équations d'Einstein pour l'univers entier).

Toutefois, les raisonnements restent valables si la courbure est la même pour tous les observateurs. Par exemple avec une topologie de sphère statique S³. Ce n'est que si la courbure spatiale varie avec l'observateur (ce qui implique forcément une courbure de l'espace-temps et non de l'espace seul) que la comptabilité avec l'invariance de c peut éventuellement être restaurée.

Transformations dans un espace compact

Nous allons maintenant essayer de déduire les transformations d'un repère à l'autre.

Pour cela, nous allons effectuer le même raisonnement que ci-dessus sur l'asymétrie de la vitesse de la lumière, mais en utilisant un signal à vitesse v quelconque.

Donc, A lance de part et d'autre un signal à vitesse v et B se déplace à vitesse V.

Les deux dernières illustrations sont exactement les mêmes et s'interprètent de la même manière. La vitesse de ce signal est donc asymétrique dans B.

Voyons maintenant le rapport entre ces différentes vitesses.

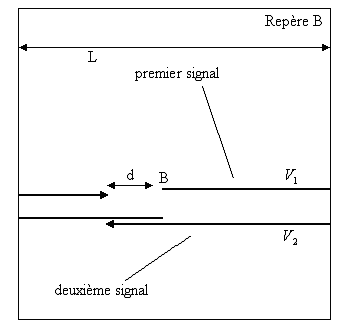
Le temps que mettent les deux signaux pour se rejoindre (pas en B, au point de croisement à gauche de B) est T.

Nous avons :

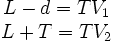
Dans le repère A, la distance d vaut simplement VL / v. Nous savons déjà que L est identique pour A et B. Comme les repères sont totalement équivalents, par symétrie, V doit être le même pour A et B. B est en mouvement à la vitesse V par rapport à A et A est en mouvement à la vitesse − V par rapport à B.

Par contre, v pourrait être perçu différemment dans B : , la fonction f_V étant a priori inconnue. Nous avons donc :

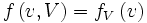
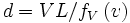
Dans A, le temps de parcourt et L / v, donc dans B :

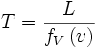
On trouve donc finalement :

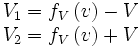
Nous savons que dans un espace compact, il n'y a pas de repère spécial. Tous les repères sont équivalents, ceci est d'ailleurs conforme au principe de relativité. La symétrie permet donc d'appliquer exactement le même raisonnement. B lance un signal à vitesse v de part et d'autre, A se déplace à V par rapport à B, et tous les raisonnements conduisent exactement aux même relations. Les relations, qui montrent comment passer du repère A au repère B, peuvent aussi être inversées afin de passer de B à A.

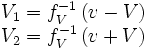
où nous avons échangé le rôle des variables, ici v est la vitesse du signal dans B et V₁ et V₂ les vitesses dans A.

Mais nous venons de dire que nous devons retrouver les relations précédentes. Donc :

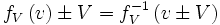
Ce qui donne :

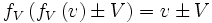
Il est clair que la seule possibilité est :

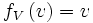
Ce qui nous donne les transformations définitives :

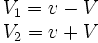
Ce sont les transformations de Galilée !

Ce qui explique les différentes conclusions auxquelles nous sommes déjà parvenus :

• Rien d'étonnant à avoir une vitesse de la lumière asymétrique dans B puisque c'est ce que prévoient les transformations de Galilée.
• Rien d'étonnant à avoir une incompatibilité entre les espaces compacts et c invariant puisque c invariant n'est pas compatible avec les transformations de Galilée.

Rappelons que les raisonnements ci-dessus sont simplistes et les conclusions pourraient être erronées.