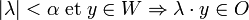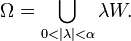Espace vectoriel topologique - Définition
La liste des auteurs de cet article est disponible ici.
Types d'espaces vectoriels topologiques
Suivant l'application qu'on en fait, on utilise généralement des contraintes supplémentaires sur la structure topologique de l'espace. Ci-dessous se trouvent quelques types particuliers d'espaces topologiques, à peu près classés selon leur gentillesse.
- Espaces vectoriels topologiques localement convexes : dans ces espaces, tout point admet une base de voisinages convexes. Par la technique connue sous le nom de fonctionnelle de Minkowski, on peut montrer que un espace est localement convexe si et seulement si sa topologie peut être définie par une famille de semi-normes. La convexité locale est le minimum requis pour des arguments géométriques comme le théorème de Hahn-Banach.
- Espaces tonnelés : espaces localement convexes où le théorème de Banach-Steinhaus s'applique.
- Espaces de Montel : espaces tonnelés où tout fermé borné est compact.
- Espaces bornologiques : espaces localement convexes où les opérateurs linéaires continus à valeurs dans un espace localement convexe sont exactement les opérateurs linéaires bornés.
- Espaces LF
- Espaces F
- Espaces de Fréchet
- Espaces nucléaires
- Espaces vectoriels normés et semi-normés : espaces localement convexes où la topologie peut être décrite par une unique norme ou semi-norme. Dans les espaces vectoriels normés, un opérateur linéaire est continu si et seulement s'il est borné.
- Espaces de Banach : espaces vectoriels normés complets. La plus grande partie de l'analyse fonctionnelle est formulée pour des espaces de Banach.
- Espaces réflexifs : espaces de Banach isomorphes à leur double dual. Un exemple important d'espace non réflexif est L1, dont le dual est L∞ mais est strictement contenu dans le dual de L∞.
- Espaces de Hilbert : ils ont un produit scalaire ; bien que ces espaces puissent être de dimension infinie, la plupart des raisonnements géométriques familiers en dimension finie s'appliquent également.
- Espaces euclidiens ou hermitiens : ceux-ci sont des espaces de Hilbert de dimension finie. Il existe alors une unique topologie conférant à l'ensemble le statut d'espace vectoriel normé. Cette configuration est étudiée dans l'article topologie d'un espace vectoriel de dimension finie.
Voisinages de l'origine
Dans toute cette section, le corps topologique K est un "corps valué" (au sens : muni d'une valeur absolue) non discret (par exemple K=R ou C), et E est un e.v.t. sur K.
Ensemble absorbant
Une partie U de E est absorbante ssi:
-
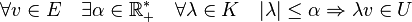
- Théorème
-
- Tout voisinage de l'origine est absorbant.
- Cela résulte de la continuité en 0 de l'application de K dans E :
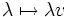
Ensemble symétrique
Une partie U de E est symétrique ssi :
-

Noyau équilibré d'une partie
Une partie U de E est équilibrée ssi :
Le noyau équilibré N d'une partie A de E est la réunion des parties équilibrées de E incluses dans A. C'est un ensemble équilibré car toute réunion d'ensembles équilibrés est équilibrée. Le noyau de A est donc le plus grand ensemble équilibré inclus dans A.
Ce noyau N est non vide ssi A contient le vecteur nul. Dans ce cas, N contient lui aussi le vecteur nul.
- Proposition
-
- Soient N le noyau équilibré d'une partie A de E, et v un vecteur de E. Pour que v appartienne à N, il faut et il suffit que pour tout scalaire
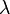
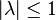
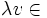
- Soient N le noyau équilibré d'une partie A de E, et v un vecteur de E. Pour que v appartienne à N, il faut et il suffit que pour tout scalaire
- En effet, v appartient à N si et seulement si, parmi les parties équilibrées contenant v, au moins l'une d'entre elles est incluse dans A, ou encore ssi la plus petite d'entre elles,
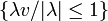
- Proposition
-
- Le noyau équilibré de tout voisinage de 0 est un voisinage de 0.
Plus précisément,
-
- tout ouvert contenant le vecteur nul contient un ouvert équilibré contenant le vecteur nul.
En effet, soit O un ouvert contenant le vecteur nul. La multiplication externe étant continue, donc continue au point
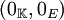
L'ensemble Ω, défini comme suit, est alors un ouvert équilibré inclus dans O :
De plus cette réunion est non vide (et contient 0) car K est non discret.