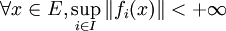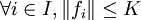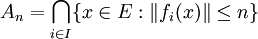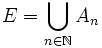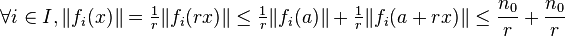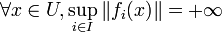Théorème de Banach-Steinhaus - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Banach-Steinhaus (aussi appelé Principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn-Banach et le théorème de Banach-Schauder, des résultats fondamentaux de l'analyse fonctionnelle. Il a été publié en 1927 par Stefan Banach et Hugo Steinhaus, mais il a aussi été prouvé indépendamment par Hans Hahn.
Il affirme qu'une famille d'applications linéaires continues définies sur un espace de Banach est uniformément bornée si et seulement si elle est ponctuellement bornée. C'est une conséquence très importante de la propriété de Baire, qui se généralise d'ailleurs aux espaces de Fréchet.
Le théorème
Énoncé
Soit E un espace de Banach et F un espace vectoriel normé. On considère une famille
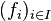
Alors
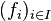
Démonstration
La preuve repose sur le fait qu'un espace de Banach est un espace de Baire, c'est-à-dire que toute réunion dénombrable de fermés d'intérieur vide est d'intérieur vide.
Considérons An l'ensemble des éléments de E tels que
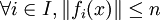
An est une intersection de fermés, c'est donc un fermé. La famille
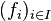
Comme E n'est pas d'intérieur vide, il existe
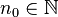
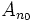
Prenons un point x de E situé dans la boule unité fermée :
c'est-à-dire :
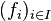
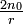
Variante "forte" de l'énoncé
On a en fait démontré le résultat suivant. Avec les mêmes notations que ci-dessus, l'alternative est :
- ou bien
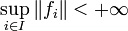
- ou bien il existe un résiduel U (c’est-à-dire une intersection dénombrable d'ouverts denses ; une telle partie est dense d'après le théorème de Baire) tel que
En effet, la démonstration précédente montre que, si
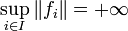
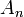
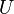
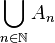
Exemples d'applications
Limite d'une suite d'applications linéaires continues
Mentionnons un corollaire très important du théorème de Banach-Steinhaus : si (fn) est une suite d'applications linéaires continues de l'espace de Banach E dans l'espace vectoriel normé F qui converge simplement vers une fonction f, alors f est également une application linéaire continue.
En effet, la linéarité provient d'un simple passage à la limite. Et pour tout
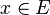
Application aux sommes de Riemann
Soit
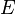
![[0,1]~](https://static.techno-science.net/illustration/Definitions/autres/8/8b3469dfda3e54ffaafe90fe9330f2f5_976c4dc1227d77a244eac5b5456f5cd2.png)
![\| f \|_\infty = \sup_{t \in [0,1]~} |f(t)|](https://static.techno-science.net/illustration/Definitions/autres/d/db0904c91c8501d15b61f211bf895b6a_3945290e9aba2fa9103eae7a97138c92.png)
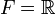
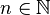
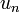
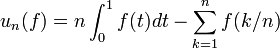
Pour toute fonction
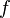
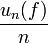
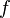
![[0,1]~](https://static.techno-science.net/illustration/Definitions/autres/8/8b3469dfda3e54ffaafe90fe9330f2f5_976c4dc1227d77a244eac5b5456f5cd2.png)
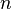
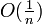
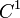
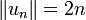
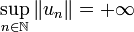
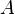
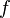
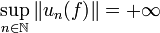
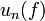
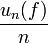
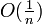
Le théorème de Banach-Steinhaus donne une preuve de l'existence d'objets vérifiant telle ou telle propriété, mais cette preuve n'est pas constructive.
Application aux séries de Fourier
Si f est une fonction (disons continue) de période
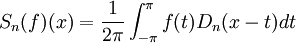
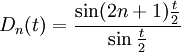
Pour n fixé, la norme de l'application
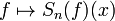
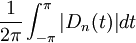
On vérifie que le nombre
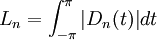
D'après le théorème de Banach-Steinhaus, il existe donc une fonction

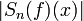
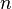


Si on utilise la version forte du théorème de Banach-Steinhaus, on voit même que l'ensemble des fonctions continues de période
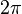

Cet argument est d'autant plus remarquable qu'il n'est pas très facile de trouver des exemples explicites.