État quantique - Définition

La notion d'état en mécanique quantique – état et mesure

En mécanique quantique, il n'est pas possible de supposer que les grandeurs physiques telles que la position ou la vitesse aient une valeur définie que l'on puisse mesurer sans perturber le système. Au lieu de cela, les observations effectuées sur un système vont modifier son état, de sorte que les résultats des mesures ultérieures vont dépendre de l'ensemble des mesures effectuées précédemment. L'état du système doit donc être défini indépendamment des grandeurs physiques observables et plutôt être vu comme une description de ce qui a été fait sur le système ainsi que des résultats obtenus lors des mesures. Pauli qualifiait « d'idéalisation de l'observateur détaché » le point de vue selon lequel l'état se résume à une liste de grandeurs physiques préexistant à la mesure. Mathématiquement, cette distinction se traduit par l'utilisation de deux objets différents pour représenter l'état et les observables du système.

De plus, on doit composer avec la nature irréductiblement aléatoire des résultats de mesure en mécanique quantique. Considérons par exemple l'équivalent quantique d'un point matériel, c’est-à-dire une particule sans spin. Les grandeurs physiques observables, ou plus simplement les observables sont en effet les mêmes dans les deux cas : la position, l'impulsion, l'énergie cinétique, l'énergie potentielle, l'énergie totale,… Supposons que l'on soit capable de préparer notre particule dans un état i bien déterminé. On peut concevoir une expérience permettant de mesurer la position, par exemple en éclairant la particule, qui donnera comme résultat : 'la particule est en r₁'. On pourrait alors en conclure que la position d'une particule préparée dans l'état i est r₁. Cependant, si l'on réitère l'expérience en plaçant à nouveau la particule dans l'état i, on obtient une autre position r₂ ≠ r₁ ! Sauf cas particulier, il en serait de même avec toute autre grandeur observable.

Au cours du temps, les physiciens ont acquis la conviction que ce fait expérimental n'était pas dû à une incertitude expérimentale lors de la mesure, ou encore à une préparation aléatoire d'une fois sur l'autre (dans un état i' i), mais plutôt que l'état ne détermine pas les résultats de mesure de manière certaine. Ceci est particulièrement illustré lors d'expériences mettant en évidence la complémentarité quantique, où malgré des mesures permettant de préparer un état précis, les résultats des mesures ultérieures restent aléatoires.

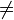
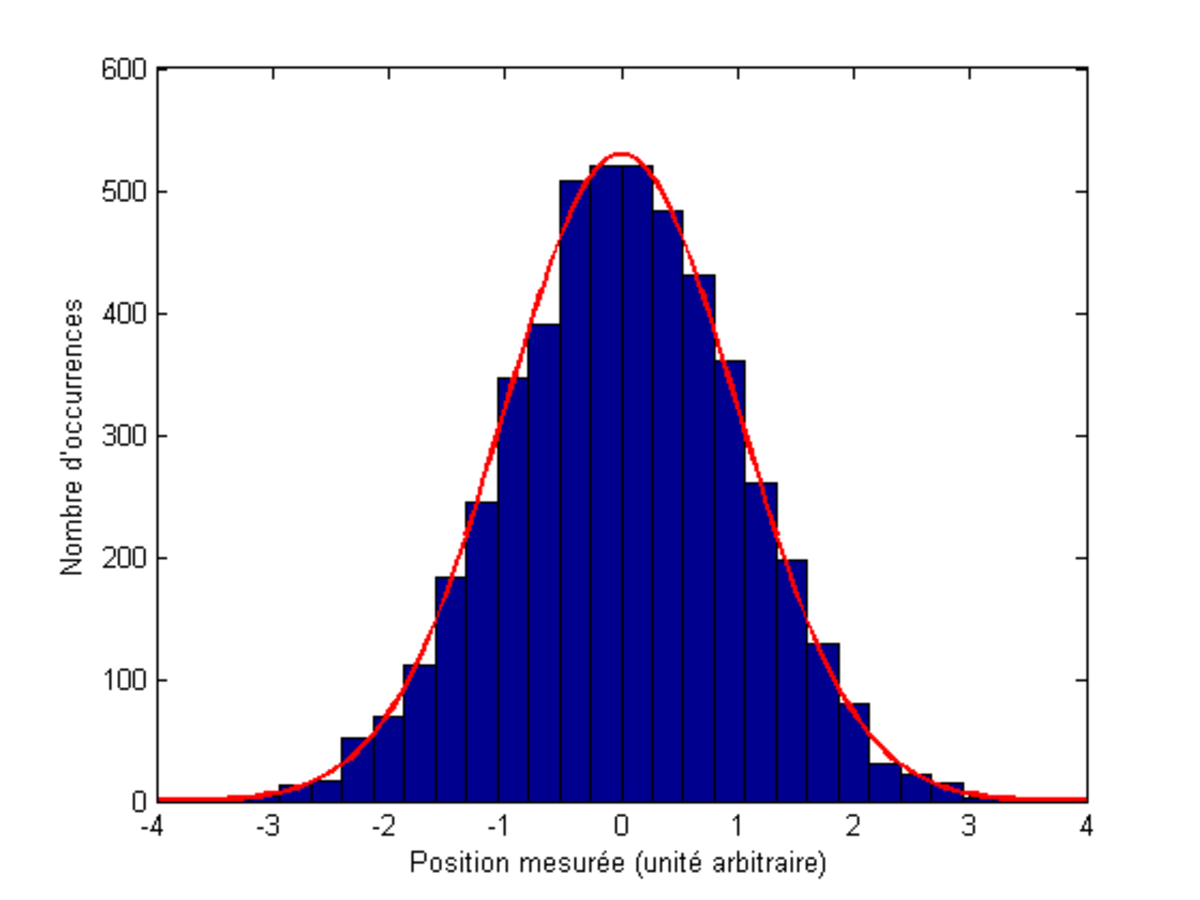
En traitant statistiquement les valeurs r₁, r₂, ... obtenues lors de mesures répétées de la position, comme dans la première figure ci-dessous, il apparaît cependant que certaines sont obtenues plus fréquemment que d'autres. Ainsi, si la valeur obtenue à l'issue de chaque mesure individuelle n'est pas connue, l'état détermine la distribution de probabilité associée à chacune des observables du système, et sa connaissance nous permet de faire des prévisions probabilistes sur les résultats de mesure. Il est alors possible de définir des grandeurs statistiques telles que la valeur moyenne de la position ou encore l'écart type de la position (notées et respectivement dans le cas de la position, et < O > et ΔO dans le cas d'une observable O quelconque, ΔO étant également appelée incertitude sur la grandeur O lorsque la particule est dans l'état i).

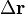
Un cas particulier intéressant correspond à des états pour lesquels l'incertitude ΔO est nulle pour une des observables O. On retrouve alors la prévision de la mécanique classique : dans un de ces états, la mesure de O donnera toujours le même résultat. Pour distinguer ces états là des autres états, ils sont appelés états propres de l'observable O. Les états propres de l'énergie totale présentent l'intérêt de ne pas évoluer au cours du temps : si une particule est dans un état d'énergie donnée, elle restera dans cet état par la suite.

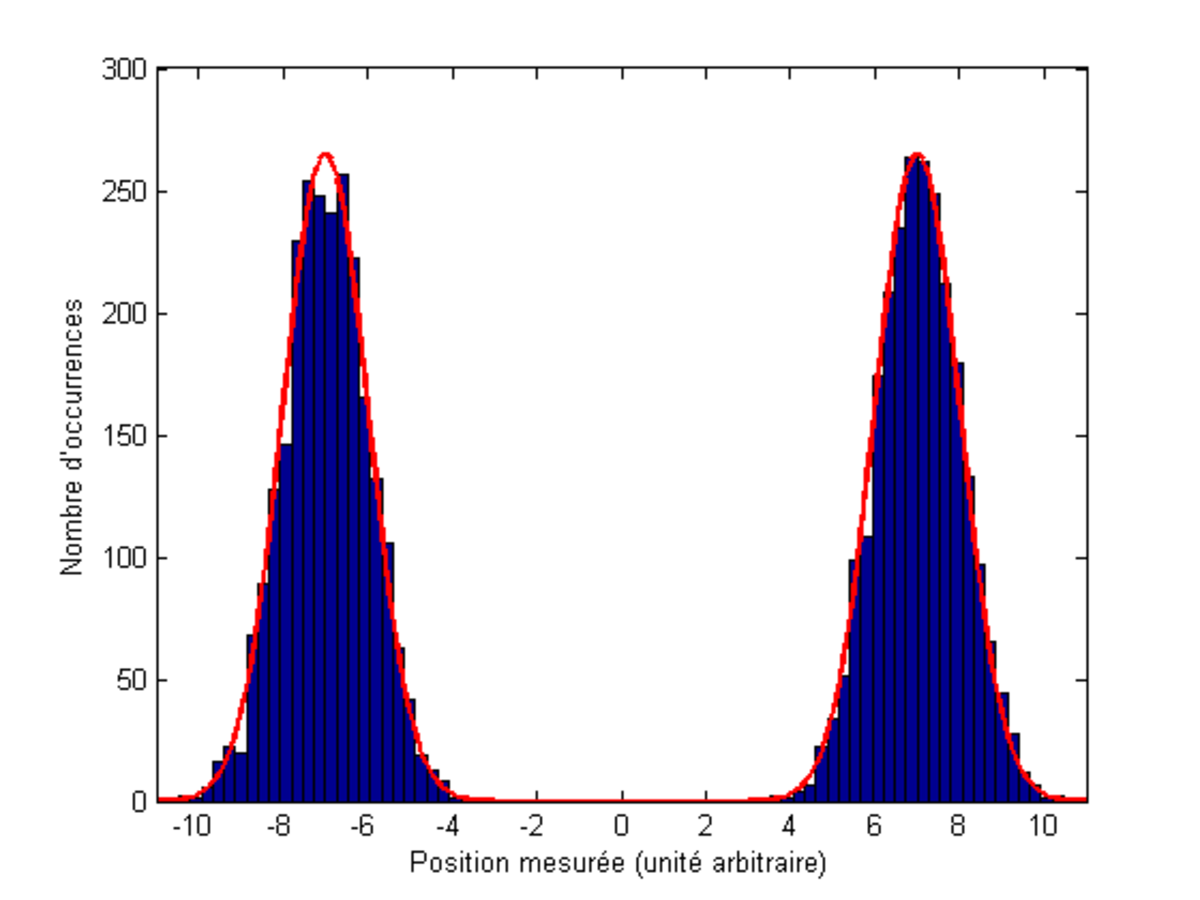
Enfin, un dernier cas particulier permet de préciser ce qui est sous-entendu lorsque l'on dit qu'une particule est dans deux états simultanément. On peut imaginer un état où la distribution de probabilité de la grandeur O est piquée sur deux valeurs. En fait, la particule n'est en réalité que dans un seul état, mais cet état quantique donnera deux résultats possibles lors d'une mesure de O.

Histogramme : statistique des résultats de N=5000 mesures de la position d'un ensemble de N particules toutes préparées dans le même état. Courbe : densité de probabilité de présence mise à la même échelle.

Mesure de la position d'un ensemble de particules dans une superposition d'états.