État quantique - Définition

La notion d'état en mécanique classique

En mécanique classique, l'état d'un système est représenté par un ensemble de grandeurs physiques à partir duquel on peut déterminer toutes les propriétés du système concerné. Par exemple dans le cas d'un point matériel, l'état est complètement décrit par la donnée du vecteur position et de la quantité de mouvement . Autrement dit, l'état du système est repéré par un point dans l'espace des phases, qui est de dimension 6 pour un point matériel. Une fois l'état du système déterminé par la mesure, on peut d'une part calculer toutes les grandeurs mesurables sur le système comme par exemple l'énergie cinétique et potentielle, mais également calculer l'état du système à un instant ultérieur grâce à l'équation fondamentale de la dynamique.

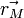
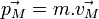
L'espace des états dépend du système considéré : si l'on considère non plus un mais N points matériels, l'état du système sera repéré par un point dans un espace vectoriel de dimension 6N, car il faut garder la trace de la position et de l'impulsion de chacun des N points matériels ; dans le cas d'un milieu continu, comme un fluide ou un solide déformable, ou encore dans le cas du champ électromagnétique, l'état du système est décrit par des champs formant un espace vectoriel de dimension infinie : potentiel scalaire et potentiel vecteur, champ de déformation, de densité massique, de vecteurs vitesse,… Là encore, d'autres grandeurs physiques mesurables peuvent être dérivées (champ de pression, forces exercées sur un objet), et l'état du système à l'instant t + τ peut se déduire de l'état du système à l'instant t à partir de lois dynamiques (Équations de Navier-Stokes, Équations de Maxwell). De manière générale, lorsque le système obéit à la mécanique lagrangienne, son état peut être décrit à l'aide des coordonnées généralisées.

Le déterminisme de l'évolution des états en mécanique classique est décrit de manière particulièrement claire par Laplace :

« Nous devons envisager l'état présent de l'univers comme l'effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaitrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux. »

— Pierre-Simon Laplace, Essai philosophique sur les probabilités (1814)

En mécanique statistique, l'état est décrit différemment : comme une distribution de probabilité sur l'espace des états. Il est toutefois compris que cette description n'est qu'une approximation liée à notre incapacité de mesurer parfaitement l'état d'un système contenant un grand nombre de degrés de liberté.

Représentation mathématique d'un état

État pur

En mécanique quantique, on représente l'état d'un système par un vecteur dans un espace vectoriel hilbertien, c'est-à-dire dans lequel est défini un produit scalaire hermitien entre deux vecteurs φ et ψ. En raison de l'importance de ces produits scalaires, on utilise la notation bra-ket introduite par Dirac pour représenter les états quantiques de manière concise et simple. Le vecteur ψ est ainsi noté et appelé ket, tandis que son vecteur dual est appelé bra et noté .

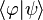
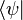
L'espace des états dépend du système considéré. Par exemple, dans le cas le plus simple où le système n'a pas de spin ou de structure interne, les états quantiques sont des fonctions telles que l'intégrale converge. Dans ce cas, ψ est appelée la fonction d'onde du système.

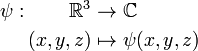
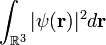
D'autre part, lorsque l'on associe deux systèmes pour en faire un seul, l'espace des états de ce système composé est le produit tensoriel des espaces des états associés aux deux sous-systèmes. (Dans le cas de deux particules identiques, il y a une restriction additionnelle, liée aux spin.)

On retrouve le déterminisme de la mécanique classique dans l'évolution de l'état quantique. C'est-à-dire que l'on peut calculer de manière déterministe comment l'état d'un système va évoluer au cours du temps (grâce à l'équation de Schrödinger), sauf lorsqu'il y a une mesure de l'état de notre système, auquel cas l'évolution n'est plus déterministe, mais probabiliste.

Il s'agit là d'une différence majeure avec la mécanique classique, qui découle du postulat de réduction du paquet d'onde et qui permet de donner une interprétation probabiliste aux états quantiques.

Représentations de Schrödinger et de Heisenberg

selon schodinger l'observable qui designe les diverses variables d'un système quantique restent constantes au cours du temps

États mixtes

Il existe d'autres représentations mathématiques de l'état quantique d'un système, la matrice densité étant une généralisation de la représentation exposée ici.

Fonction de Wigner