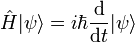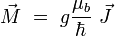Expérience de Stern et Gerlach - Définition

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

Plaque commémorative de l'expérience portant l'effigie des deux physiciens au siège de la Physikalische Verein à Francfort-sur-le-Main

Expérience de Stern et Gerlach

L'expérience de Stern et Gerlach est une expérience de mécanique quantique démontrant l'existence du spin. L'expérience a été mise au point par Otto Stern et Walther Gerlach en février 1922.

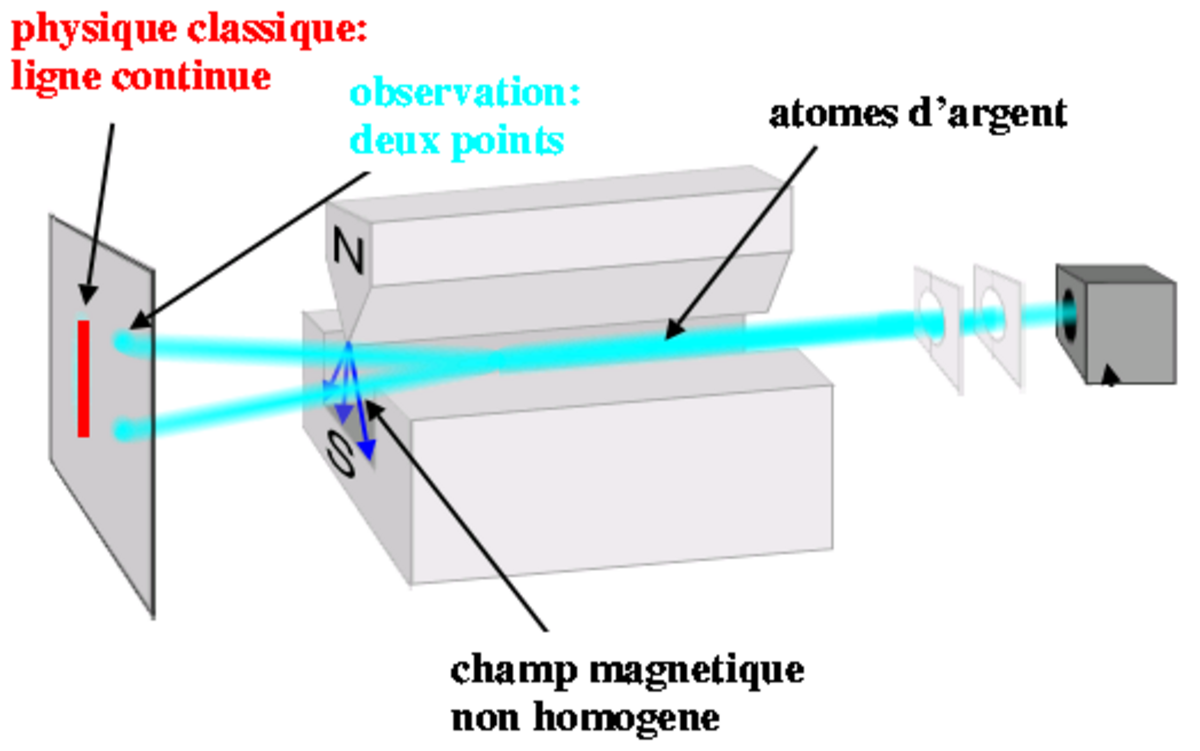
Elle consiste à faire passer des atomes d'argent dans un champ magnétique non uniforme de direction verticale. Les atomes d'argent dans leur état fondamental ayant un moment cinétique nul, son moment magnétique orbital associé est nul également. Ainsi, le faisceau ne devrait classiquement pas subir l'influence du champ magnétique.

Cependant, l'expérience montre que le faisceau se sépare en deux. On ne peut donc pas attribuer ce résultat au moment cinétique orbital. On est alors obligé d'introduire le moment cinétique de spin, ou plus simplement spin, qui n'a pas d'équivalent classique.

Dans le cas de l'atome d'argent, qui est de spin 1/2, celui-ci ne peut prendre que 2 valeurs discrètes : +1/2 et -1/2, d'où la séparation en deux faisceaux.

Démonstration

De manière générale, à un moment cinétique d'une particule de charge q et de masse m est associé un moment magnétique:

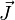
où g est le facteur de Landé et est le magnéton de Bohr.

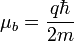
Pour l'atome d'argent dans l'état fondamental, entraîne . Le moment magnétique orbital est nul.

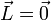
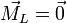
Comme la force qui s'exerce sur un moment magnétique vaut : où est le champ magnétique extérieur, alors la force qui devrait s'exercer sur le faisceau d'argent est nulle. Le faisceau ne devrait alors pas être dévié.

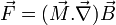
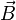
Cependant, il existe en fait un moment cinétique de spin de telle sorte que , moment magnétique de spin, est non nul.

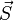
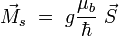
De plus, comme ce spin ne peut prendre que deux valeurs, dans le cas d'un spin 1/2, alors la force qui s'exerce sur le faisceau vaut pour les atomes dont la projection du spin sur l'axe z vaut 1/2 et pour les atomes dont la projection du spin sur l'axe z vaut -1/2. On rappellera que la projection sur l'axe z est purement arbitraire.

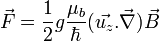
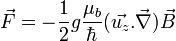
Ainsi, on observe bien la séparation du faisceau initial en deux faisceaux.