Extension algébrique - Définition

Définitions et premières propriétés

Soit K un corps et L une extension de corps.

• Un élément l de L est dit algébrique sur K si et seulement s'il existe un polynôme non nul à coefficients dans K ayant l pour racine.

• L'extension L est dite algébrique si et seulement si tout élément de L est algébrique sur K.

• L dispose d'une structure d'espace vectoriel sur K. Si cette structure confère à L une structure d'espace vectoriel de dimension finie, on parle alors d' extension finie. La dimension est souvent notée [L:K] et est appelé le degré de l'extension.

• Une extension algébrique L telle que les puissances d'un de ses éléments l forment une famille génératrice de L (en tant que K-espace vectoriel) est dite simple.

• L'ensemble F des nombres algébriques de L sur K est un sous-corps de L appelé fermeture algébrique de K dans L.

Les extensions algébriques L possèdent quelques propriétés élémentaires:

• Si L/K est une extension finie, alors L est une extension algébrique de K.
• Si L/K est une extension finie et si K/H est une extension finie, L est une extension finie de H de degré [L:K].[K:H].

• Si L/K est une extension algébrique et si K/H est une extension algébrique, alors L est une extension algébrique de H.

Approche par l'exemple

Une extension simple construite à l'aide d'un sur-corps

L'idée est de construire le plus petit sur-corps L de contenant le réel . Puisque L est stable par la multiplication et par l'addition, tout élément de la forme avec a et b appartenant à appartient à L.

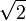
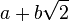
On montre facilement que l'ensemble K de ces éléments s'écrivant avec a et b dans forment eux-mêmes un corps commutatif. Par la propriété de minimalité de L, on conclut que K=L. K est stable pour l'addition:

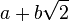
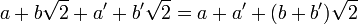
Les éléments neutres de l'addition et de la multiplication sont clairement élément de l'ensemble.

Tout élément possède dans K un opposé:

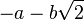
Le produit (c'est là la seule finesse) est aussi stable par la multiplication.

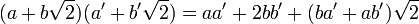
Enfin, tout élément non nul de K admet un inverse:

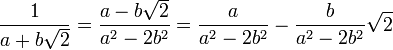
remarque : pour a et b rationnels non tous les deux nuls a² - 2b² est non nul car n'est pas un rationnel.

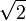
Par construction, ce corps est le plus petit sous-corps des nombres réels contenant à la fois les nombres rationnels et . Plus petit signifie ici que tout sous-corps des nombres réels contenant à la fois les nombres rationnels et contient aussi L=K.

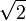
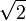
L possède un certain nombre de propriétés intéressantes:

• L est un espace vectoriel sur les nombres rationnels. Cet espace est de dimension finie égale à 2. On parle alors d'extension quadratique.
• L, en tant qu'espace vectoriel possède une base constituée de puissances de , à savoir (1, ). On parle alors d'extension simple.
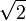
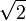
• Si x est un élément de L alors la famille (1, x, x²) est liée car de cardinal supérieur à celui de la dimension. Il existe donc un polynôme à coefficients dans les nombres rationnels ayant x pour racine.

Une approche intuitive montre qu'une structure de type L est un candidat intéressant pour bâtir une théorie. En revanche, il n'est pas très satisfaisant d'avoir utilisé un sur-corps des nombres rationnels, à savoir les nombres réels, pour une telle construction. Si, dans la pratique, quel que soit le corps K il est toujours possible de montrer l'existence d'un sur-corps Ω possédant les propriétés nécessaires, il existe une autre approche qui ne nécessite pas l'existence d'un tel sur-corps a priori.

Construction à l'aide des polynômes

On démontre que l'ensemble des polynômes à coefficients dans : est un anneau commutatif unitaire euclidien et principal. On peut créer une notion de divisibilité, parler de division euclidienne, de polynômes premiers (irréductibles) et d'identité de Bézout. On peut même définir, comme dans , une congruence modulo P(X) (où P(X) est un polynôme) de la manière suivante: P₁ et P₂ sont congrus modulo P(X) ssi il existe un polynôme S(X) tel que P₁(X) − P₂(X) = S(X)P(X).

Cette congruence est une relation d'équivalence compatible avec l'addition et la multiplication dans . On peut donc construire l'ensemble quotient . Cet ensemble est encore un anneau commutatif unitaire. Si P(X) est un polynôme irréductible, par exemple égal à X²+1, l'identité de Bézout permet de dire que L est un corps. L'ensemble L défini précédemment est un corps. On plonge naturellement le corps dans ce corps L en associant à chaque réel, sa classe d'équivalence. Si l'on note traditionnellement i la classe de X, alors L est une extension quadratique des nombres réels telle que l'équation X²+1 = 0 admette deux racines i et -i. L correspond donc à la construction des nombres complexes.

Si P(X) est choisi comme étant égal à X²-2 et si le corps est choisi égal à celui des nombres rationnels, on obtient une extension des rationnels isomorphe au sous-corps des nombres réels du paragraphe précédent.