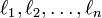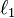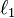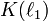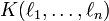Extension algébrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Motivations - Définitions et premières propriétés - Approche par l'exemple - Extension algébrique et sur-corps - Extension algébrique et polynôme - Extensions particulières

Extension algébrique et polynôme

Article détaillé Corps de rupture

Soit K un corps et P(X) un polynôme irréductible de degré n à coefficients dans K. Alors il existe une extension algébrique de K contenant au moins une racine de P(X) et minimale pour cette propriété. Cette extension est appelée corps de rupture de P(X). Cette extension est unique à K-isomorphisme près et elle est finie de degré n sur K.

Soit P(X) un polynôme non-constant sur K. Alors il existe une extension finie L' de K telle que le polynôme P(X) soit scindé dans L' , c'est-à-dire qu'il se décompose en produit de polynômes de degré 1 à coefficients dans L' . On dit plus intuitivement que P(X) a toutes ses racines dans L' . Si on prend L' minimale pour cette propriété, alors elle est unique à K-isomorphisme près. On l'appelle alors corps de décomposition de P(X).

Soit P(X) un polynôme non-constant sur K, alors il existe une extension finie L' de K tel que le polynôme P(X) admet toutes ses racines dans L' .

Procédons par récurrence sur le degré d de P(X). Si d=1, on peut prendre L' = K. Supposons d au moins égal à 2 et que la propriété est vraie pour tout polynôme de degré d-1 (sur un corps quelconque).

Soit K₁ un corps de rupture de P(X). Alors P(X) s'écrit comme P_1(X)P_2(X) avec P_i(X) appartenant à K₁[X], P₁(X) de degré 1 et P₂(X) de degré d-1. Par hypothèse de récurrence, il existe une extension finie L' de K₁ telle que P₂(X) ait toutes ses racines dans L' . Il suit que P(X) a toutes ses racines dans L' . Ce qui achève la démonstration puisque L' est une extension finie de K.

Extensions particulières

Extension quadratique

article détaillé: Extension quadratique

Les extensions quadratiques interviennent notamment pour la résolution des problèmes de l'antiquité sur les nombre constructibles. Ces nombres forment un corps inclus dans les nombres réels et stable par la fonction racine carrée, c’est-à-dire que la racine carré d'un nombre constructible positif est aussi constructible. Une identification du plan euclidien et des nombres complexes montre que les nombres constructibles forment le plus petit corps contenant i le nombre imaginaire pur, les nombres rationnels et stable par la fonction conjuguée et la fonction racine carrée.

Un tel corps peut se construire à l'aide d'une suite infinie d'extensions quadratiques des nombres rationnels (K₀, K₁, ... , K_n, ...) où K₀ est le corps des nombres rationnels et K_n est une extension quadratique du corps K_n-1 si n est strictement positif. Tout nombre constructible s'obtient comme élément d'un corps construit à partir d'une suite finie de corps construits comme extension quadratique du corps précédent dans la suite. On parle alors de tour d'extensions quadratiques.

Une fois cette propriété démontrée, il devient aisé de résoudre les problèmes de l'antiquité comme la duplication du cube. En effet, la duplication du cube demande de construire un nombre d dont le polynôme minimal est de degré trois. Or la dimension de toute extension contenant d est du type 2^p ou p est un entier. Comme le degré du polynôme minimal d'un élément d'une extension algébrique divise toujours la dimension de l'extension algébrique, le problème n'a pas de solution.

Une approche analogue montre l'impossibilité de la résolution dans le cas général de la Trisection de l'angle par les méthodes de la règle et du compas et permet de déterminer les polygones réguliers constructibles.

Extension de Galois

Article détaillé : Extension de Galois

Un autre outil est essentiel pour l'analyse des extensions L d'un corps K, il correspond aux automorphismes de L laissant le corps K invariant. L'ensemble des automorphismes munis de la loi de composition interne des fonctions forme une structure de groupe. Cet outil est particulièrement efficace dans le cas des extensions finies par exemple sur le corps des rationnels dans le cas d'un corps de décomposition. Un élément de ce groupe restreint à un ensemble de racines d'un polynôme correspond à une permutation de cet ensemble de racines. Dans le cas des extensions finies, il correspond à un groupe fini appelé Groupe de Galois.

Pour que cet outil soit pleinement pertinent, il faut en fait que les polynômes minimaux de l'extension n'aient pas de racines multiples. Ce qui est toujours le cas pour des extensions sur les corps des rationnels ou pour les extensions dans le cas d'un corps de caractéristique nulle. Dans ce cadre, il est par exemple possible de montrer qu'il existe un élément a dit primitif tel que l'extension soit une extension simple égal à K(a). Il faut de plus que l'extension contienne suffisamment de racines. Il faut en fait que le cardinal du groupe soit égal à la dimension de l'extension. Si ces deux hypothèses sont vérifiées, on parle alors d'extension de Galois.

Le groupe de Galois permet de comprendre finement la structure de l'extension. Par exemple, il existe une bijection entre ses sous-groupes et les sous-corps de l'extension. Il est utilisé pour la détermination des polygones constructibles à la règle et au compas ou pour le théorème d'Abel sur la résolution d'équations polynomiales par radicaux.

Clôture algébrique

Article détaillé : Clôture algébrique

Il existe une extension algébrique particulière, celle qui ne possède pour polynôme minimaux que les polynômes de degré 1. C'est l'extension pour lequel tous les polynômes de degré différent de zéro admettent au moins une racine. Dans le cas des nombres réels, l'extension finie décrite plus haut suffit pour obtenir une clôture algébrique. Dans le cas des nombres rationnels, la clôture algébrique s'obtient soit comme l'ensemble des nombres complexes qui sont algébriques (on vérifie aisément que cet ensemble forme un corps), soit comme union dénombrable d'une suite croissante d'extensions. On prouve que la clôture algébrique du corps des nombres réels est le corps des nombres complexes au moyen du théorème de d'Alembert-Gauss ; il n'existe aucune preuve connue purement algébrique, l'utilisation d'outils topologiques est jusqu'à maintenant toujours nécessaire.

Si la clôture algébrique des nombres réels est un espace de dimension deux sur les réels, en revanche la clôture algébrique des nombres rationnels est de dimension infinie sur ce corps. Il suffit pour s'en convaincre de remarquer que pour tout entier, il existe un polynôme minimal de degré strictement supérieur à cet entier, la dimension est donc supérieure à tout entier.

Dans le cas général, tout corps possède une clôture algébrique et c'est une extension du corps dont on est parti. En général, on doit utiliser l'axiome du choix pour prouver ce théorème. La preuve nécessite en effet une suite infinie d'extensions algébriques emboîtées.

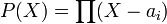
Il n'existe aucun corps fini algébriquement clos. En effet, si on considère le produit $P(X)=\prod (X - a_i )$ , où les $a i$ parcourent l'ensemble du corps fini $K$ , alors $P + 1$ est un polynôme non constant ne possédant aucune racine dans $K$ .

Enfin, soit une extension finie $L$ d'un corps $K$ ; elle est alors isomorphe à un sous-corps de toute clôture algébrique $Ω$ de $K$ . Pour s'en convaincre, il suffit de considérer une suite $\ell_1, \ell_2, \dots, \ell_n$ d'éléments engendrant $L$ . Si elle ne contient qu'un élément $\ell_1$ , on note $P (X)$ le polynôme minimal de $\ell_1$ dans $K$ . Soit $λ 1$ une racine de $P$ dans $Ω$ , alors $K(\ell_1)$ dans $L$ est isomorphe à $K (λ 1)$ dans $Ω$ . Dans le cas général, $K(\ell_1,\dots,\ell_n)$ est une extension de $K (λ 1)$ engendrée par $n - 1$ éléments. Un argument de récurrence permet de conclure.