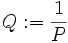Construction des nombres complexes - Définition

Le but de cet article est de présenter, d'une part la construction, facile, des nombres complexes, et d'autre part, la démonstration, parfois un peu plus compliquée, qu'il s'agit bien d'un corps algébriquement clos.

Définition en tant que corps valué

En tant que simple corps, les complexes sont aisés à définir; cela fait appel à la notion d'extension algébrique par adjonction de racines :

La classe de X est notée i (parfois, par exemple en électricité, les physiciens préfèrent utiliser j, et réservent la lettre i à une intensité). Elle vérifie comme on le souhaitait la relation: i² = − 1.

Ceci définit une extension des nombres réels, de dimension 2 (on peut donc bien écrire de façon unique tout nombre complexe sous la forme a + bi où a et b sont des réels). On va la munir de la norme d'extension algébrique la plus naturelle dans ce cadre: . Elle prolonge bien celle des réels, et en tant qu'espace vectoriel de dimension finie sur , on a bien un espace complet.

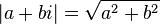
Démonstration de la clôture algébrique

via les fonctions holomorphes et le théorème de Liouville

On raisonne par l'absurde : soit P un polynôme non constant n'ayant aucune racine dans le corps des complexes. Alors on peut définir son inverse sur tout entier. Q est développable en série entière au voisinage de tout point, donc holomorphe. De plus, en module, P(z) tend vers l'infini lorsque z tend vers l'infini, donc Q(z) tend vers zéro en l'infini. Q étant de plus continue, elle est bornée sur entier. Étant holomorphe, elle est constante, par le théorème de Liouville. Contradiction.