Extension algébrique - Définition

• Soit P(X) un polynôme irréductible de degré n sur K, L une extension finie de dimension n sur K contenant une racine du polynôme et L' une extension contenant au moins une racine de P(X). Alors L' est une extension de L.

Soit β une racine de P(X) dans L' . Considérons alors l'application j de L dans L' définie par :

L'application j est un morphisme d'espace vectoriel, il suffit donc de démontrer qu'elle est aussi un morphisme pour la multiplication interne. Soit a et b deux éléments de L, alors il existe deux polynômes A(X) et B(X) tel que a = A(α) et b = B(α). Les égalités suivantes montrent que j est aussi un morphisme pour l'addition.

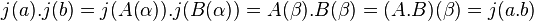
Ce qui termine la démonstration.

• Soit P(X) un polynôme sur K, alors il existe une extension finie minimal L' de K tel que le polynôme P(X) admet toutes ses racines dans L' . Minimal signifie ici que toute extension F contenant toutes les racines de P(X) est une extension de L.

Le polynôme P(X) est le produit d'un polynôme scindé et de polynômes irréductibles de degré supérieur ou égal à 2.

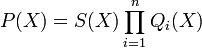
Si n est égal à 0, c’est-à-dire si le polynôme P(X) est scindé, alors K est l'extension minimale tel que le polynôme soit scindé. Dans le cas contraire, démontrons la proposition par récurrence sur le degré p du polynôme produit des polynômes irréductibles.

Si p est égal à 2, ce qui est la plus petite valeur possible par construction, alors n est égal à 1 et la proposition précédente montre l'existence d'un corps L tel que Q₁(X) admette une racine. Ce polynôme est alors scindé car il est de degré 2. La première proposition montre que F est une extension de L.

Supposons la propriété vraie pour toute valeur inférieure ou égal à p. Supposons alors que le produit des polynômes irréductibles soit de degré p+1. Il existe alors une extension K₁ tel que le polynôme Q₁(X) admette au moins une racine. Sur K₁le polynôme Q₁(X) est alors produit S'(X).Q'₁ d'un polynôme scindé et d'un polynôme de degré strictement inférieur à celui de Q₁(X). Par hypothèse de récurrence il existe une extension finie L de K₁ minimale tel que le polynôme P(X) est scindé sur L. L est de dimension [K₁:K].[L.K₁] sur K.

Montrons enfin que F est une extension de L. F est une extension de K₁ qui contient toutes les racines du polynôme produit de S(X), S'(X), Q'₁ et des Q_i. Par hypothèse de récurrence, c'est donc une extension de L. Et la proposition est démontrée.

• Si L est une extension algébrique d'un corps K et si (a₁, a₂, ..., a_n) est une famille de L, alors il existe un plus petit sous-corps de L contenant la famille, et ce sous-corps est une extension finie de K.

Soit P_i(X) le polynôme minimal de a_i à coefficient dans K. Ce polynôme existe car a_i est algébrique sur K. Le produit de tous ces polynômes admet pour racines tous les éléments de la famille. L'idéal annulateur de cette famille dans K(X) est donc non vide. Soit P(X) le polynôme générateur de cet idéal. Il existe un sous-corps de L isomorphe au corps de décomposition de P(X). D'après la proposition précédente, ce sous-corps est de dimension finie et est le plus petit contenant la famille, et la proposition est démontrée.

• Si K est une extension algébrique d'un corps H et si L est une extension algébrique de K, alors L est une extension algébrique de H.

Soit l un élément de L. Il existe un polynôme à coefficients dans K annulant l car L est algébrique sur K. Notons (a₁, a₂, ..., a_n) la famille des coefficients du polynôme, notons F le corps H(a₁, a₂, ..., a_n) F est de dimension finie sur H, F(l) est de dimension finie sur F et l est inclus dans F(l) qui est de dimension [F(l):F].[F:H] sur H. Et donc, l est inclus dans une extension de dimension finie de H ce qui démontre la proposition.

• Le degré du polynôme minimal de l divise [L:K].

Considérons la plus petite extension K₁ de K contenant l. Sa dimension est égale au degré du polynôme minimal n de l. Or L est aussi une extension de K₁. L'égalité suivante démontre alors le résultat: [L:K] = n.[K₁:K]