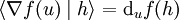Forme différentielle de degré un - Définition
La liste des auteurs de cet article est disponible ici.
Formes différentielles sur un ouvert de l'espace euclidien
Modèles locaux
Les modèles locaux en géométrie différentielle sont les ouverts d'espaces vectoriels de dimension finie. Les objets et leurs propriétés peuvent se définir sur de tels espaces ; leurs invariances par difféomorphismes autorisent ensuite le passage aux variétés.
Etant donné un espace vectoriel normé réel ou complexe E (en général de dimension finie, mais pas nécessairement) et U un ouvert de E, une forme différentielle ω (de degré 1) de classe
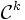
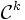
En dimension finie le choix d'une base de E permet d'exprimer les 1-formes différentielles. Plus exactement, si une base e=(e1,..., en) de E est donnée, il lui est associée la base duale de E* : les éléments de celle-ci sont notés
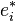
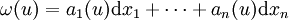
où a1,..., an sont des fonctions de classe
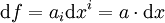
Exemple : Pour une fonction f de classe
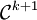
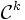
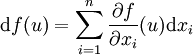
Notamment, dans le cas où l'application f est l'application qui à x associe sa i-ième coordonnée :
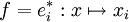
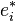
Changement de coordonnées
L'algèbre linéaire montre comment l'expression d'une forme linéaire dans une base dépend de cette dernière. Plus exactement, son expression dans une nouvelle base se déduit par l'action de la transposée de la matrice de passage. Si e et f sont deux bases de E, et si
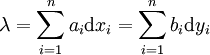
En géométrie différentielle se rencontrent des changements de coordonnées locales qui correspondent à des difféomorphismes. Il apparaît nécessaire de comprendre comment un difféomorphisme agit sur une 1-forme différentielle définie sur un ouvert d'un espace vectoriel. Si
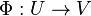
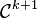

![\Phi^*\omega(u)=\omega\left[\Phi(u)\right]\circ d\Phi(u)](https://static.techno-science.net/illustration/Definitions/autres/4/45aa553e49aa7f8709f40a17254a3b9e_828fcb3ce676faea7b47697d892583cd.png)
L'expression des 1-formes différentielles a été choisie pour que les calculs puissent être menés sans difficulté. Si e et f sont des bases de E, et que ω s'exprime dans la base f:
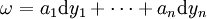
alors l'expression de Φ * ω dans la base e est :
![\Phi^*\omega=a_1\mathrm{d}\Phi_1+\dots+a_n\mathrm{d}\Phi_n=\left[\sum_{i=1}^na_i\frac{\partial \Phi_i}{\partial x_1}\right]\mathrm{d}x_1+\dots+\left[\sum_{i=1}^na_i\frac{\partial \Phi_i}{\partial x_n}\right]\mathrm{d}x_n](https://static.techno-science.net/illustration/Definitions/autres/0/07842b4bffaa839ba6c23e85b86fdd3d_3d0a837d0090e09e9a184b1f3c52696a.png)
Définition sur les variétés
Une variété M de classe Ck + 1 peut être décrite comme un ensemble d'ouverts de l'espace
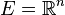
Lien avec les champs de vecteurs
Si E est muni d'un produit scalaire (et de dimension finie), il existe un isomorphisme entre E et son dual. On peut donc établir une correspondance entre formes différentielles et champs de vecteurs : si ω est une forme différentielle sur U, il existe un unique champ de vecteurs X sur U tel que
-
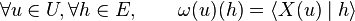
À la notion de forme différentielle exacte ayant f pour primitive correspond alors celle de champ de gradient, dérivant du potentiel f :
-